
During the Fall of 2022, MEGL ran a 6 project program with 40 participants between faculty, graduate, and undergraduate students. The six research/visualization groups are titled:
- The Stability of Icebergs and other Floating Objects
- Random 3D Polyforms
- Resolving Neural Ideals
- Applications of Geometric Desingularization
- Experimenting with Moduli Spaces
- Tipping In Climate Impact Models
In addition to these projects, MEGL ran a public engagement group which we refer to below as Outreach.
The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries.
We concluded with an end of term symposium and a poster session, sharing progress and results of our research. To learn more, see below:
Faculty Mentor: Professor Daniel Anderson and Professor Evelyn Sander
Description: We explore the stability of floating objects at a two-fluid interface through mathematical modeling and experimentation. Our models are based on standard ideas of center of gravity, center of buoyancy, and Archimedes’ Principle extended to the notion of a two-fluid scenario. We investigate floating shapes with two-dimensional constant cross sections and identify analytically and/or computationally a potential energy landscape that helps identify stable and unstable floating orientations. We compare our analyses and computations to experiments on floating objects designed and created through 3D printing. Additionally, the paper includes open problems for further study for topics.

Graduate Research Assistant: Patrick Bishop
Research Interns:
- Gabriela Castaneda Guzman
- Gina Thomas
- Mark William Brant
Faculty Mentor: Professor Ben Schweinhart and Professor Erika Roldan
Description: We explore polyforms, a class of shapes constructed by joining together identical polytopes connected by at least one of their faces. Specifically, this project studies random polyforms composed of cubes strongly connected by their two-dimensional square faces. In our work, we’ve developed algorithms for generating, shuffling, enumerating two and three dimensional polyforms. (You can try shuffling some polyforms yourself in your browser at https://dgramop.xyz/blocks.html.) We’ve improved the computational efficiency of code to scale linearly with the size and number of shuffles as well as sample from non-uniform distributions using percolation probabilities. From these algorithms, we generate cubical complexes and use tools from persistence theory to observe how the geometric characteristics of our polyforms change as with how we generate them. Future work involves shuffling larger size polyforms and creating large datasets to observe mixing time in the three-dimensional case.
The project builds on work of David Aristoff (Colorado State) and Erika Roldán (TU Munich/EPFL) to study random two-dimensional polyforms (called polyominoes), and will be conducted in collaboration with Dr. Roldán.

Graduate Research Assistant: Shrunal Pothagoni
Research Interns:
- Bharath Vemuri
- Dhruv Gramopadhye
- Ethan Reis Concepcion
- Khoi Tran
- James Serrano
Faculty Mentor: Professor Rebecca Rebhuhn-glanz and Professor Hugh Geller
Description: The purpose of this endeavor is to study the construction of the canonical form of neural ideals. Neural ideals are algebraic objects which are associated with collections of neurons firing in a brain. A specific example which has a nice geometric interpretation is collections of place cells, which fire to tell an animal where they are in space. Neural ideals provide a means for us to study the properties of the stimulus space- the space of possible stimuli causing neurons to fire- using tools from commutative algebra. The canonical form of a neural ideals encodes the minimal relations of subsets of the stimulus space in a way which is convenient to return to studying the geometric and topological properties of the stimulus space. This semester, we wrote a program which will compute the canonical form of a given neural ideal, and another program which generates various classes of neural ideals in canonical form. These programs made it convenient to compute free resolutions of our neural ideals. Free resolutions offer a way to study how the betti numbers of our resolutions change based on the canonical form of neural ideals.
Graduate Research Assistant: John Kent and Swan Klein
Research Interns:
- Connor William Poulton
- Gabriel Lumpkin
- Justin Roy Cox
Faculty Mentor: Professor Matthew Holzer
Description: For this project, we are examining a certain system found in Bramburger \& Henderson , which describes a coupled reaction-advection-diffusion system with a large parameter $\rho$. In their paper, Bramburger and Henderson also present present a theorem that states that the critical speed $c^*(\rho)$ is in the range of $(\frac{3}{2})^{1/3} \leq \liminf_{\rho \to \infty}\frac{c_*(\rho)}{\rho^{1/3}} \leq \limsup_{\rho \to \infty}\frac{c_*(\rho)}{\rho^{1/3}} \leq \sqrt{3}$, which we have narrowed down to a singular value: $\lim_{\rho \to \infty} \frac{c_*(\rho)}{\rho^{1/3}} = \sqrt[3]{\frac{3}{2}}$. When letting the viscosity, $\nu = 0$, there exists traveling wavefront solutions for wave speed $c \geq c_*(\rho)$. This yields a set of ODEs that were derived by Bramburger and Henderson:
\begin{equation}
\begin{split}
\dot{T} &= -cT + UT + \frac{1}{2\rho}U\\
\dot{U} &= \frac{\rho}{U-c}T(1-T)
\end{split}
\end{equation}
By applying several techniques for rewriting ODEs and letting $\epsilon = 0$ we find two fixed points: one at the origin $(0,0)$ and the other $(1,c)$. In this way, we could find the exact value that was approximated in Bramberger and Henderson’s paper, but due to a lack of hyperbolicity at $(1,c)$ we needed to use the Implicit Function Theorem to ensure that solutions would not be lost for $\epsilon > 0$. To this end, we use a quasi-homogeneous blow-up to an ellipsoid and use projective charts to analyze the system more easily. Graphic illustrations of these projective charts are displayed below. Due to the trapping regions and existence of the heteroclinic orbit, our theorem holds true for $\rho \to \infty$.
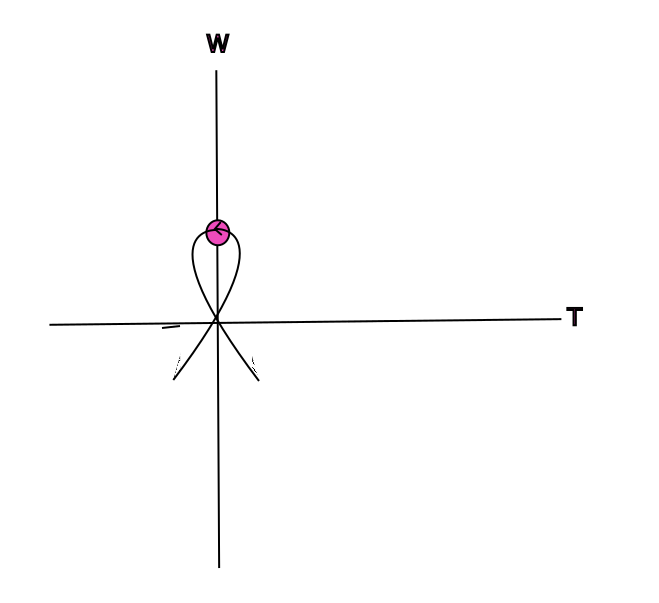
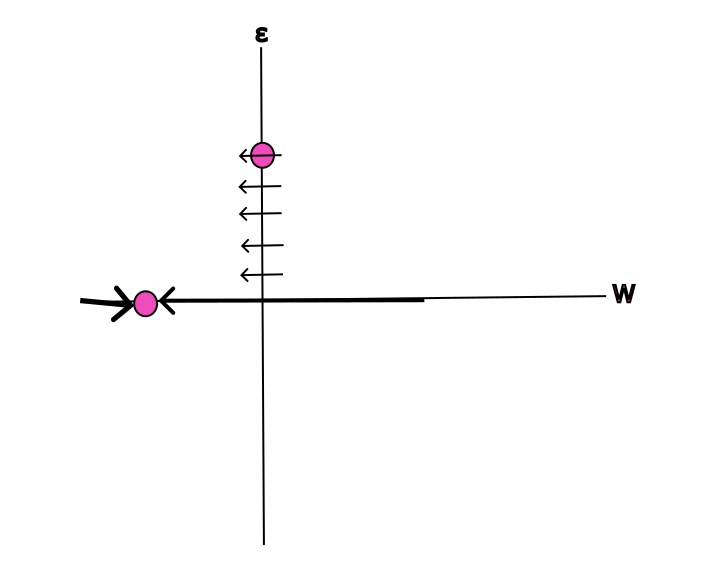
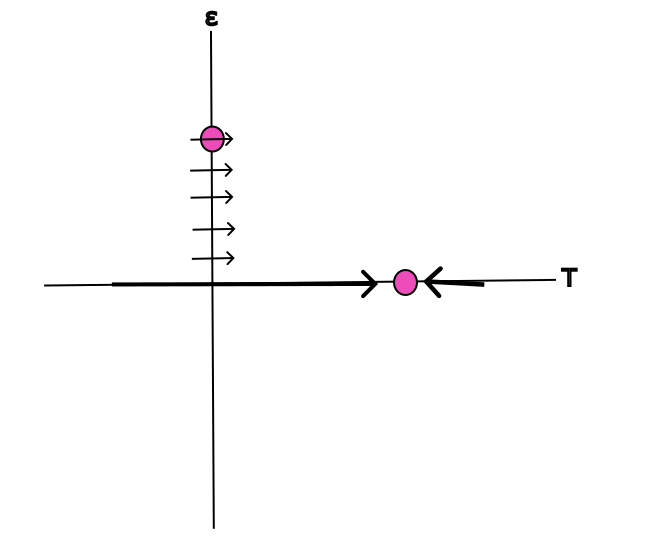
Graduate Research Assistant: Matthew David Kearney
Research Interns:
- David Wigginton
- Katie Tuttle
- Samuel Molseed
Faculty Mentor: Professor Sean Lawton
Description: In fall 2022 we studied families of dynamical systems over finite fields. In particular we looked at an action of the classical groups (with an emphasis on the general linear group) on multivariate polynomials. We focused on describing the orbits in the linear and quadratic cases, as well as finding forms for fixed points, describing maximal orbits, and outlining asymptotic behaviors. In the spring we will continue this work by finishing the quadratic case and examining higher degrees, describing fixed points in full, sharpening bounds on when maximal orbits occur, and fully describing asymptotic behavior. In addition to these extensions of the current work, we aim to look at the “local dynamics” of our system. If time permits we may examine the action of other classical groups in more depth, examine other fields, and look at the behavior in projective space.
Graduate Research Assistant: Michael Merkle
Research Interns:
- Holly Miller
- Violet Nguyen
- Ziqi Zhan
Faculty Mentor: Professor Emmanuel Fleurantin and Professor Chris Jones
Description: Tipping from one apparently stable state of a system to another can be activated by a too rapid rate of change in some underlying parameter. The presence of noise can also force tipping to occur and, moreover, these two effects can work together. The rate change will come from either the background warming of the climate or some sudden shift in conditions triggered by climate change. Tipping between two saddle equilibria is associated with a heteroclinic connection between these saddle points. Particular challenges emerge in the complex systems that arise in climate where the basin boundary (tipping threshold) becomes intricate, such as the stable manifold of a periodic orbit. In this project, we will seek to capture the connecting orbit by deliberately computing invariant sets. This will involve rigorous computations of invariant sets and their visualization. There is the possibility of enrolling in an Udemy course to get more familiar with specific software for computational purposes. We will develop the project in models that arise in areas such as the carbon cycle, permafrost melting, peat fires and hurricanes.
Graduate Research Assistant: Martha Hartt
Research Interns:
- Dmitri Shatov
- Joanna Ro
- Aidan Self
Outreach Manager: Martha Hartt
Description: MEGL offers outreach activities to the community every semester. To fulfill our mission of outreach, we need your help. Participants will deliver, refine and help develop mathematical outreach activities which inspire a passion for mathematics. Check out our website for examples of MEGL outreach activities.
Graduate Assistant: Matthew David Kearney
Undergraduate Interns:
- Merold Saffa
- Aidan Self
- Joanna Ro
- Salina Tecle
