MEGL is running an 8 project program with 56 participants between faculty, graduate research assistants, and undergraduate research interns. The research projects are titled
- Universal Cycles in Higher Dimensions
- Embeddings of a semi-homogeneous tree in the hyperbolic disk.
- Monte Carlo, Las Vegas, and Quantum Algorithms for Quantum Systems
- Kelly criterion
- Biological Locomotion via Surface Tension
- Topology of Neural Networks
- Finite 2-groups
- Hyperbolic Knots in Thickened Surfaces
In addition to the research projects, MEGL is running an Outreach program, which exposes K-12 students to important mathematical concepts through visualizations and hands-on activities.
The research teams are meeting weekly to generate empirical data which helps them form and explore mathematical conjectures based on observed patterns.
At the end of the semester, the research teams will have the opportunity to present their findings at a poster session followed by a Symposium. For project descriptions and names of the researchers involved, click the boxes below.
Faculty Mentor: Rachel Kirsch
Prerequisites: returning students only
Description: A De Bruijn cycle is a compact cyclical listing of all the words of length n. For example, the sequence 0011, considered cyclically, is a De Bruijn cycle for n = 2 because the subwords of length 2 beginning in its first, second, third, and fourth positions, respectively, are 00, 01, 11, and 10, which are all of the binary words of length 2. More generally, a universal cycle for a family of combinatorial objects of rank n runs through each element of the family exactly once. Universal cycles have extensive applications in computer science, coding theory, cryptography, and computational biology. This research project examines higher-dimensional analogues of universal cycles such as perfect maps, also known as De Bruijn tori.
Graduate Research Assistant: Matthew Kearney
Research Interns:
- Stefan Popescu
- William Carey
Faculty Mentor: Flavia Colonna
Pre-requisites: Math213
Description: The proposed project is a follow-up of the MEGL project under way titled “Embeddings of a homogeneous tree in the hyperbolic disk”, in which most of the goals that we set out to pursue have been accomplished. Specifically, the following objectives have been reached or are close to completion.
- A visualization of the geometric construction of an optimal embedding of a homogeneous tree of even degree in the unit disk has been obtained. By an optimal embedding we mean a mapping of the tree into the disk such that the boundary of the tree covers the entire unit circle and the edges of the tree are geodesic curves of the same hyperbolic length.
- Using the even degree case as a model, a similar visualization in the odd degree case was obtained based on a conjecture suggested from the even-degree case. The theoretic proof of the optimality, not yet completed, has not been treated in a published paper.
The goals for the continuation of the project are two-fold:
- Provide a rigorous proof of the optimality in the odd-degree case.
- Treat the embedding problem in the case of a semi-homogeneous tree, that is an infinite tree whose vertices have two degrees, that alternate as one moves along the tree. We conjecture that it will be possible to obtain an optimal embedding but there might be an extra degree of freedom involved, unlike the homogenous case treated so far.
- We plan to run some simulations for semi-homogeneous tree in which the alternating degrees are 4 and 3 to see if our conjecture is likely before delving into the technical aspects of the construction. These would require an appropriate group representation for this type of tree to pave the way for the formulas that ought to yield the vertices of the embedded tree.
Graduate Research Assistant: Madeline Horton
Research Interns:
- Arpan Das
- Connor Poulton
- Tate Fitzmaurice
Faculty mentor: Michael Jarret
Prerequisites: Math213
Description: An essential tool in understanding the power of quantum computing is understanding its best classical competition. This can lead to insights into where the power of quantum computation comes from, as well as novel classical and quantum algorithms. In this project, students will analytically investigate numerical algorithms presently used for understanding quantum systems, in order to understand their running time and complexity. Students may be asked to develop novel classical/quantum algorithms, either provable or heuristic.
Graduate Research Assistants: John Kent and Anthony Pizzimenti
Research Interns:
- Andy Miller
- Mark Dubynskyi
- Raghu Guggilam
Faculty: Douglas Eckley
Prerequisites: nothing beyond the usual Math213 pre-requisite
Description: This project will apply the Kelly Investment Criterion to various real-world investing and/or gambling scenarios.
The goal of the project is to bring together several concepts from statistics and economics in a way that that is conducive to visualization. The project can be done entirely either in spreadsheet or in R / Python.
Assignment
- Research the Kelly Investment Criterion via a textbook that I will supply
- Present the development of the Criterion
- Apply the Criterion in various settings, including a setting that leads to the Proebsting Paradox
- Present results
The statistical concepts involved are:
- Utility theory
- Maximizing a function
- Ruin theory
- Modeling the stock market
- Jensen’s Inequality
Research Interns:
- Bemnet Bekele
- James O’Hanlon
- Tiffany Sun
Faculty Mentors: Evelyn Sander and Dan Anderson
Description: Our goal in this project is to use a combination of analysis, computation, and experiments with 3D printed floating objects in order to better understand the method in which biology solves the problem of locomotion via the use of surface tension.
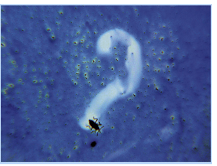

Photo credits: Left: Burton, Cheng, and Bush “The cocktail boat” Int. Comp. Biol. 54 969-973 (2014). Right: Bryant Kelly Flickr (CC BY 2.0).
Graduate Research Assistants: Brandon Barreto-Rosa and Patrick Bishop
Research Interns:
- Daniel Horvath
- Mariah Tammera
- Max Werkheiser
- Sarah Wendt
Faculty: Benjamin Schweinhart
Prerequisites: Some knowledge of data science, CS 112, and Math 203
Recommended: Math 321 and 431 would be nice but not required
Description: A Neural Network may be geometrically interpreted as a nonlinear function that stretches and pulls apart data between vector spaces. If a dataset has interesting geometric or topological structure, one might ask how the structure of the data will change when passed through a neural network. This is achieved by explicitly viewing the dataset as a manifold and observing how the topological complexity (i.e., the sum of the Betti numbers) of the manifold changes as it passes through the activation layers of a neural network. The goal of this project is to study how the topological complexity of the data changes by tuning the hyper-parameters of the network. This enables us to possibly understand the relationship between the structural mechanics of the network and its performance. Research interns will be expected to meet twice a week to learn the relevant literature, implement neural network architectures, visualize numerical results, and develop heuristics.
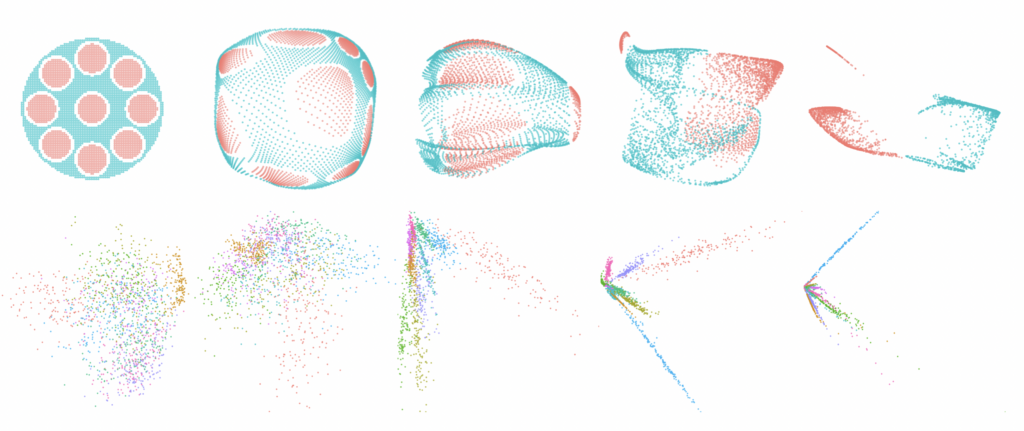
Graduate Research Assistants: Shrunal Pothagoni and Justin Cox
Research Interns:
- Alex Martinez
- David Wigginton
- Eugenie Ahn
- Finn Brennan
Faculty: Casey Blacker
Prerequisites: Math 321
Description: The aim of this project is to understand the structure of finite 2-groups. A 2-groupis a certain hybrid of a group and a category. Informally, a category is a set equipped with abstract relations between its elements. The elements are called objects and the relations are called arrows or morphisms.
Whereas a group describes multiplication of elements in a set,

a 2-group describes multiplication of both objects and arrows in certain categories.

Intriguingly, while the symmetries of a structured set form a group, the symmetries of a special structured category forms a 2-group. A 2-group may thus encode a configuration of symmetries that are at once subtler and more expressive than those described by groups.
In this project, we seek to extend various constructions and results of group theory to the 2-group setting.Here are three potential lines of inquiry:
1. Every finite abelian group is the direct sum of cyclic subgroups. Is every finite abelian 2-group the direct sum of cyclic sub-2-groups? How should abelian, direct sum, and cyclic be defined for 2-groups?
2. Cayley’s theorem asserts that every group arises as a subgroup of the symmetries of some set. Does every finite 2-group so arise as symmetries of some category?
3. Does an analogous version of the first isomorphism theorem hold for 2-groups? How should homomorphism, kernel, image, and quotient be defined for 2-groups?
We will first consider strict 2-groups. These have the benefit of being characterized in terms of two ordinary groups and two ordinary group homomorphisms. Time permitting, we will then broaden our attention to general finite 2-groups.
Graduate Research Assistants: Ethan Clelland and Michael Merkle
Research Interns:
- Anthony Vu
- Morgan Schuman
- Nick Lear
Faculty: Rose Kaplan-Kelly
Prerequisites: Multivariable calculus. No background in knot theory is expected.
Description: In this project, we will be investigating tilings, knots, links, and surfaces. Imagine taking a few pieces of string, tying them up, and then gluing the loose ends together in pairs. The result is a mathematical link(except that we think of the string as having no thickness, so its cross section is a point). Each individual piece of string that we started with is a component of the link and when a link has only one component we call it a knot. We can build links from tilings by turning the edges of the tiling into strands of the link and the vertices of the tiling into crossings.
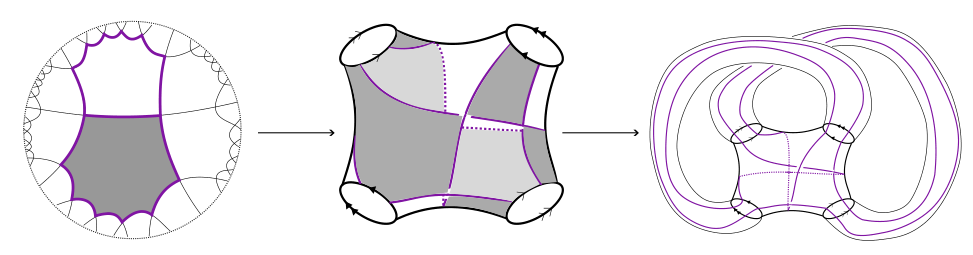
A thickened surface is a surface crossed with an interval. For example, to imagine a thickened torus,we could picture a pool noodle with its ends glued to each other. The complement of a link in a thickened surface is the space left over after we remove the components of the link. We say that a link is hyperbolic if its complement admits a complete metric of constant curvature -1. A way to think of negative curvature is to consider lines of sight. Here our lines of sight diverge quickly. We can see this on the hyperbolic pentagons in Figure 2. Near a vertex, geodesic segments have a small angle between them, but as we move along the sides of the pentagons these segments quickly bend away from each other.
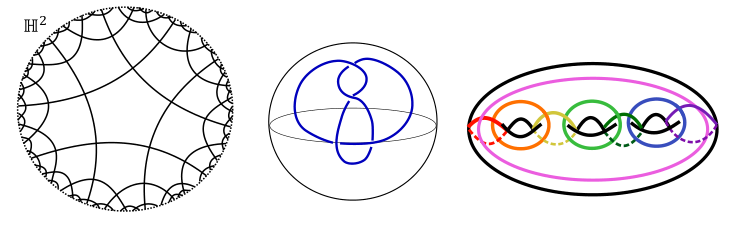
Right: A link diagram on a genus 3 surface.
In this project, we will explore questions such as:
1. Can we construct knots in any genus thickened surface from tilings consisting of one or two types of polygons?
2. How many links built from tilings with one or two types of polygons are there with diagrams on a genus 2 surface?
Graduate Research Assistants: Gabe Lumpkin and Kiefer Green
Research Interns:
- Antonio Alt
- Haboon Yusuf
- Nicholas Maranto

