To schedule an activity please email us at [email protected]
What are some different ways to sort shapes? How can we fit shapes together to cover an entire area? And how should we color that area of shapes? In this activity, students will investigate Polygons, Tilings and Coloring Theorems in a very hands-on way.

Topics covered:
- Shape classification
- Polygons vs. non-polygons
- Names of polygons based on the number of sides
- Regular polygons
- Tilings
- Which regular polygons tile
- (if applicable) Study of angles
- Colorings
- The 4 Color Theorem
Prerequisites:
- Knowledge of what shapes are
- Knowledge of Straight vs. Curvy
- (optional) experience with shape classification
Main takeaway: Serious mathematics emerges from exploring and experimenting with shapes.
Aligns with Virginia’s Standards of Learning: 1.MG.2, 2.MG.3 and 3.MG.4.
Created by Martha Hartt
The students learn about prime numbers, the “atoms” of the counting numbers. Students learn to factorize numbers geometrically: They arrange poker chips into rectangular arrays and realize that the side lengths are the factors. By repeating this process, they can decompose a number into its prime factors and draw a “number tree” to keep track of their work. When they’re finished, they create paper plate Monsters that represent the prime number decomposition of their original number. Then they try to decode each others’ Monsters to figure out what numbers they represent. This activity is inspired by a book (with the same title) by Richard Schwartz.

Topics covered:
- Prime vs. Composite (Rectangle) Number classification
- Pattern recognition
- Factor trees
- Multiplication of prime factors to get original numbers
Prerequisites:
- Familiarity with whole numbers
- Familiarity with Rectangles
- (Recommended) Some exposure to Prime Numbers
- Ability to multiply single digit numbers
- (Recommended) Previous experience with number classification of some sort
- Familiarity with basic patterns (odd and even numbers)
Main takeaway: Prime numbers are the building blocks of all whole numbers.
Aligns with Virginia’s Standards of Learning: 5.NS.2.
Created by Sean Lawton
What is the shape of a bubble? What happens when two, three or more bubbles are joined together? This workshop will give a brief introduction to the geometrical and physical properties of bubbles and soap films. You will have time to create your own bubbles and play with 3D objects to see how a soap film attaches to cubes, pyramids, and fun curves.

Topics covered:
- Surface tension
- Minimizing properties of Bubbles
- Soap films in polyhedrons and curved wires.
Prerequisites:
- Familiarity with bubbles
- Familiarity with spheres, triangles, polygons, cube, tetrahedron, pyramids.
- Some geometry: Angles, distances, area
- (Recommended) Idea about surface tension
- (Recommended) Good 3D imagination
Main takeaway: Surface tension forces bubbles to be efficient and minimize surface area
Created by Ros Toala
How big is REALLY big? How can we imagine numbers like a Googol, which has 100 zeros? Using a certain rule, how far can we get in a certain number of steps? Students gain an intuition for the sheer magnitude of the real numbers by stepping through different growing number patterns using contextualized interactive activities. This activity is inspired by a book (with the same title) by Richard Schwartz.

Topics covered:
- Growth rates in different contexts: Simple counting, linear, square, exponential, (if time) factorial.
- Scientific Notation through the Scale of the Universe.
Prerequisite:
- Familiarity with whole numbers
- Familiarity with addition and multiplication
- (Recommended) Familiarity with powers of 2
- (optional) Familiarity with growth
- (optional) Familiarity with functions
- (optionlal) Scientific Notation
Main takeaway: Recognize patterns based on how fast they grow.
Aligns with Virginia’s Standards of Learning: 4.PFA.1, and 5.PFA.1.
Created by Sean Lawton and Jack Love
A 1×1 square has area 1. A 2×2 square has area 4. Can we make a square with area 2? Students begin to make sense of irrational numbers by engaging in a variety of activities that showcase all the places they pop up in our lives. After drawing the elusive square of area 2, students discover the role that pi has while throwing straws at a felt wall in a live simulation of Buffon’s Needle. They then learn about nature’s affinity for a particular irrational ratio and create their own Fibonacci spiral.
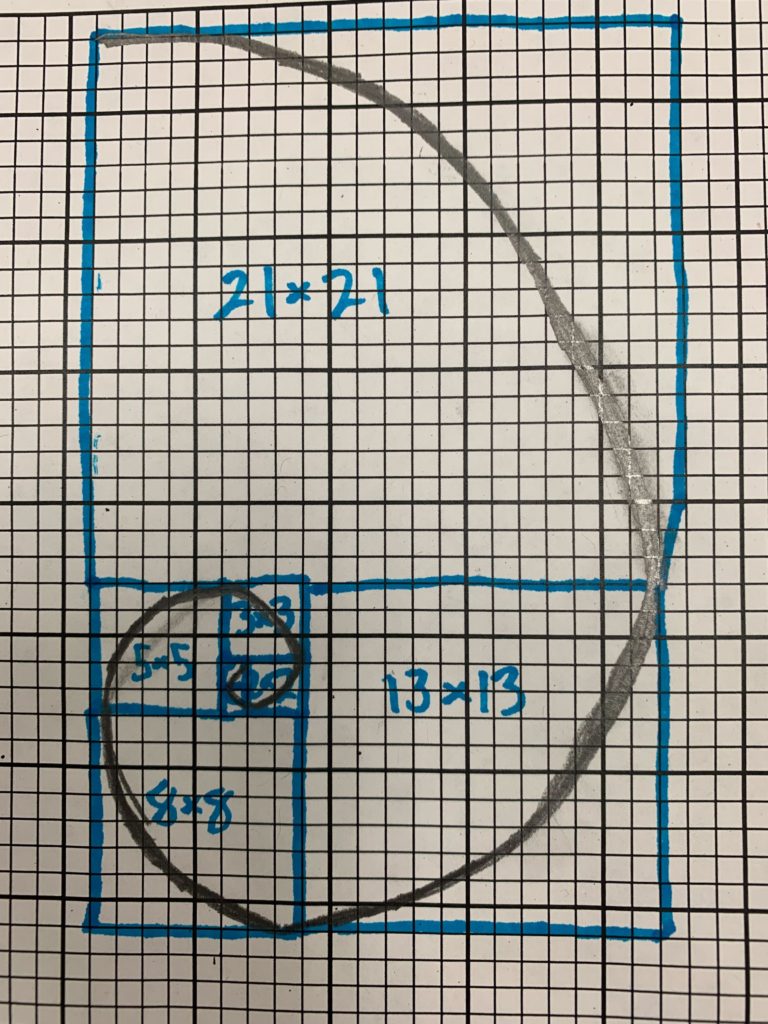
Topics covered:
- Representing numbers as fractions
- Whole numbers
- Terminating decimals
- Non-terminating decimals
- How to represent numbers that cannot be represented as fractions:
- Square root of 2 (using squares)
- Pi (using circles)
- The golden ratio (using spirals)
Prerequisites
- Very familiar with fractions, capable of adding/multiplying them
- Very familiar with decimals, capable of adding/multiplying them
- Exposure to fraction/decimal conversion
- Have good number sense
- (Optional) Have heard of pi and perimeter of a circle
- (Optional) Knowledge of square roots
- Familiarity with basic shapes: Square and its area, drawing circles.
Main takeaway: Not all numbers can be neatly represented using symbols we’re familiar with.
Aligns with Virginia’s Standards of Learning: 7.NS.2, 7.NS.3 and 8.NS.1.
Created by Aidan Donahue, Susan Tarabulsi, Martha Hartt, Harry Bray, and Lujain Nsair
It stands on its own but also is a great sequel to Really Big Numbers. Students use a variety of interactive puzzles and games, and activities to explore the strange world of the infinite. What is infinity plus one? Are there different sizes of infinity? Join us to find out! This activity is inspired by a book by Richard Schwartz (titled Gallery of the Infinite).
Topics covered:
- Definition of finite and countably infinite
- Input/output machines
- Arithmetic involving infinity
- Different types of infinity
Prerequisites:
- Decent number sense
- (Optional) Experience with input/output machines
Main takeaway: Infinity works differently from regular numbers
Created by Sean Lawton, Jack Love, and Anton Lukyanenko
Students will gain a firmer understanding of how computers work by investigating search algorithms. They will then learn about the difference between classical algorithms and quantum algorithms and get to explore the idea of superposition by playing a familiar game.
Topics covered:
- Black boxes
- Algorithms
- Searching Algorithms
- Quantum Physics
Prerequisites:
- Basic Knowledge of Computers
- Knowledge of “Input/Output” Machine
- Basic Knowledge of Probabilities
- Basic knowledge of Measurement
Main takeaway: Quantum Computing takes advantage of tiny particles to do things quicker than regular computers.
Created by Martha Hartt
Is there more to math than numbers? Can we “multiply” things that aren’t numbers? How about the motions (or, symmetries) of a snowflake? What does a symmetry multiplication table look like, and what can it tell us about the motions a snowflake makes as it falls? How are snowflake symmetries the same as numbers? How are they different? In this activity students create their own paper snowflakes and experiment with them to explore these questions. Along the way we discover beauty hiding just beneath the surface, and find there is more to math than we thought!

Topics covered:
- How to fold a paper to achieve 5-fold and 6-fold symmetry.
- Symmetries can be though as operations
- (optional) What is a ‘multiplication table’ of symmetries.
Prerequisites:
- Regular polygons
- Lines of symmetry
- Mirror and rotational symmetry
Aligns with Virginia’s Standards of Learning: 6.MG.4, 7.MG.3 and G.RLT.3.
Created by Sean Lawton
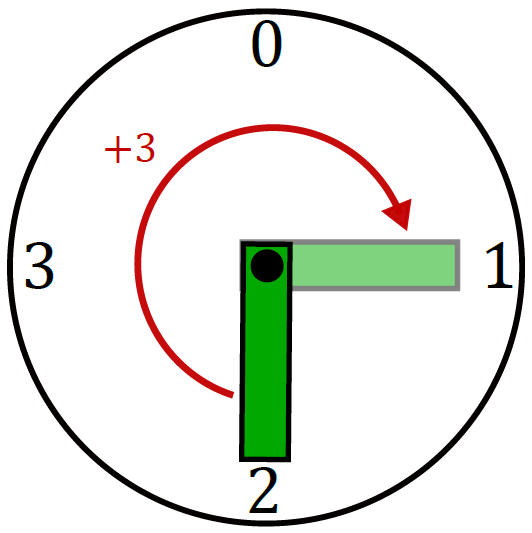
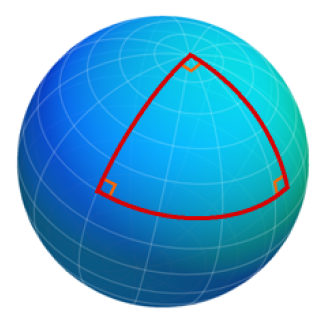
The students learn what they’ve been taught in school isn’t necessarily the truth! They experience simple mathematical “facts” being turned on their heads by changing the context in which they appear. Through kinesthetic activities and manipulatives including balloons and special clocks, they see that 2+2 isn’t always 4, that triangles aren’t what they thought they were, that cutting a strip of paper in half does not necessarily disconnect it, that some squares have negative area, and that it is possible to divide by 0.
Topics covered:
- Activity 1: Regular arithmetic vs Modular (clock) arithmetic
- Activity 2: Spherical geometry. How is it different from plane geometry?
- Activity 3: Mobius strips.
- Activity 4 (if time): Can negative numbers have a square root? Imaginary numbers.
Prerequisites:
- Activity 1:
- Basic Number Sense
- Familiarity with whole numbers and simple addition
- Activity 2:
- Sum of angles in a triangle
- Familiarity with the sphere and great circles.
- Activity 3:
- Spatial coordination and intuition.
- Activity 4:
- Familiarity with squares and area formula
- (Optional) familiarity with complex numbers
- Familiarity with basic arithmetic
Main takeaway: Mathematical statements also depend on context.
Created by Sean Lawton


We first teach participants about the “Cinderella” of geometry–the least appreciated and most beautiful. We then teach participants how to crochet so they can make their own exotic shapes in yarn. This activity is inspired by a book by Daina Taimina .
Topics covered:
- Crocheting a flat disk
- Introduction to three different geometries: Euclidean, Spherical, Hyperbolic.
- Circles in the three geometries: Continuos version, Discrete version, crochet version.
- How to crochet the different geometries
Prerequisites:
- Area of a circle.
- Familiarity with counting patterns: Linear and exponential growth.
- (Optional) Familiarity with 3D cartesian coordinates
- (Optional) Familiarity with Spherical coordinates
- (Optional/Recommended) Experience with crochet
Main takeaway: Area of circles in Euclidean geometry grow linearly, area of circles in Hyperbolic geometry grows exponentially.
Created by Sean Lawton
Ask Us About:
- Follow-up lesson plans for all activities for interested teachers/students.
- Training for Geometry Labs and other interested mathematicians to reproduce MEGL outreach in your location.

