MEGL ran a 6 project program with 45 participants between faculty, graduate research assistants, and undergraduate research interns. The research projects were titled
- Universal Cycles in Higher Dimensions
- Optimal Embedding of a Homogenous Tree in the Hyperbolic Disk
- Principal Minors of the Fourier Matrix
- Monte Carlo, Las Vegas, and Quantum Algorithms for Quantum Systems
- Proebsting’s Paradox
- Biological Locomotion via Surface Tension
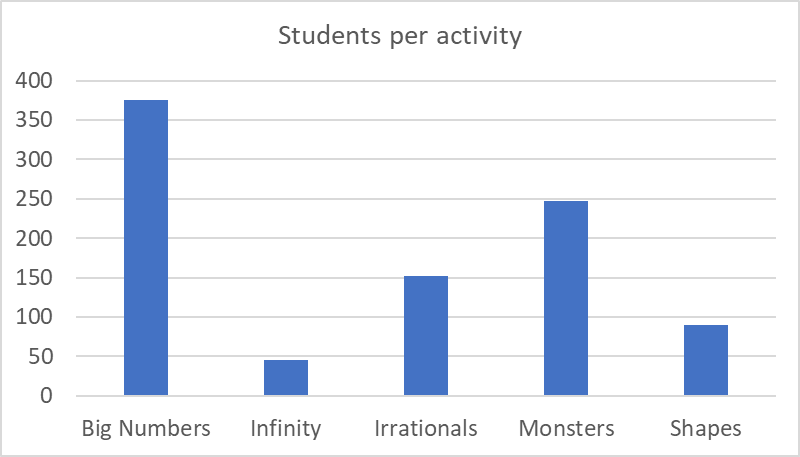
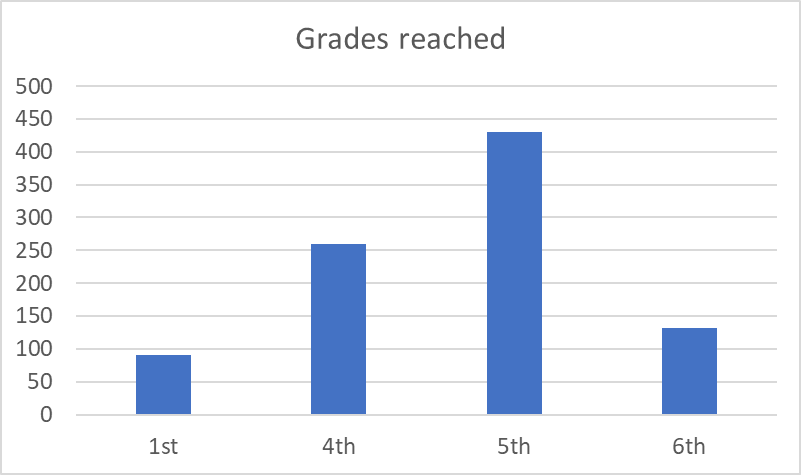
In addition to the research projects, MEGL is running an Outreach program, which exposes K-12 students to important mathematical concepts through visualizations and hands-on activities.
The research teams met weekly to generate empirical data which helps them form, and then explore mathematical conjectures based on observed patterns.
At the end of the semester, the research teams presented their findings at a poster session followed by a Symposium, which included talks from a keynote speaker and two honors thesis presentations. For project descriptions and names of the researchers involved, click the boxes below.
Faculty: Rachel Kirsch
Description: We familiarized ourselves with concepts such as de Bruijn cycles, de Bruijn tori, de Bruijn families, universal partial cycles, and other topics related to combinatorics. Among some of our most significant findings were what we believe to be the first universal partial tori (or “uptori”). For example:
“`
⋄ 0 0 1
1 1 0 0
1 1 0 0
“`
An uptorus is an array of characters (including a wildcard in at least one position) that is viewed cyclically and covers every rectangular window with a specified height and width exactly once (like a de Bruijn torus, which does not have wildcards, does). We also discovered a method to generate much larger uptori using universal partial cycles.
Graduate Research Assistant: Matthew Kearney
Research Interns:
- Charles Landreaux
- Stefan Popescu
- William Carey
Faculty Mentor: Flavia Colonna
Description: In a 1994 paper I wrote with Joel M. Cohen, we solved the problem of how to embed a homogeneous tree of even degree in the unit disk so that the boundary of the tree covers the entire unit circle and such that the edges of the tree are geodesic curves of the same length with respect to the hyperbolic metric. We proved that the explicit construction of such a tree can be carried out using ruler and compass. The purpose of this project is two-fold:
· Provide a visualization of the above geometric construction.
· Using the even degree case as a model, produce a similar construction in the odd degree case, which has not been treated in a published paper.
At the start of the project, we plan to cover the following basic concepts:
· boundary of an infinite tree
· how to view a homogeneous tree as a group
· the hyperbolic disk in the plane
We will then go over the construction described in the paper to obtain a visualization. Then have fun extending this to the odd-degree case.
Graduate Research Assistant: Madeline Horton
Research Interns:
- Calvin Dorn
- Connor Poulton
- Tate Fitzmaurice
Faculty: David Walnut The aim of this project is to explore a conjecture involving principal minors of the Fourier matrix (also called the DFT matrix). The conjecture is that for every natural number N, there exists a permutation σ of {0, 1, . . . , N − 1} such that every principal minor of the matrix WσN is nonzero. Here WσN is the DFT matrix WN whose rows have been permuted by σ. The conjecture is true if N is a prime number (Chebotarev’s Theorem) and we confirmed it up to N = 30 numerically. Over the course of this semester, we gave proofs for three theorems that give us tools for working with principal minors of the Fourier matrix. Some remaining conjectures remain, first that it seems that all principle minors are non-zero for the identity permutation if N is a product of distinct primes and we found a permutation that seems to work when N is the power of a prime.
Graduate Research Assistant: Shrunal Pothagoni
Research Interns:
- Katie Tuttle
- David Wigginton
- Finn Brennan
Faculty Mentor: Michael Jarret-Baume
Description: In the Fall 2023 semester, we studied Quantum Markov Chain Monte Carlo methods. We learned about using Metropolis-Hastings Algorithms with the Ising Model. We began researching the Negative-Sign Problem, which is known as the biggest bottleneck in Quantum in numerical simulations of quantum models, on the basis that it seems to have been mischaracterized.
Next semester, we hope to find ways to aid physics researchers in curing or easing the Negative-Sign Problem, such as categorizing occurrences of the problem and pairing them with optimal methods for curing and easing the problem.
Here is visualization of a known Monte Carlo method that we implemented during the semester:
Graduate Research Assistant: Anthony Pizzimenti
Research Interns:
- Mark Dubynskyi
- Raghavendra Guggilam
Faculty: Douglas Eckley
Project Description:
Background
This project will apply the Kelly Investment Criterion to various real-world investing and/or gambling scenarios.
The goal of the project is to bring together several concepts from statistics and economics in a way that that is conducive to visualization. The project can be done entirely either in spreadsheet or in R.
Assignment
1 Research the Kelly Investment Criterion via a textbook that I will supply
2 Present the development of the Criterion
3 Apply the Criterion in various settings, including a setting that leads to the Proebsting Paradox
4 Present results
The statistical concepts involved are:
Utility theory
Maximizing a function
Ruin theory
Call options on common stock
Black-Scholes option pricing
Research Interns:
- Dylan Sierra Ornelas
- Nathaniel Marshall
- Sarah Wendt
Faculty Mentors: Evelyn Sander and Dan Anderson
Description: Our goal in this project is to use a combination of analysis, computation, and experiments with 3D printed floating objects in order to better understand the method in which biology solves the problem of locomotion via the use of surface tension.
Photo credits: Left: Burton, Cheng, and Bush “The cocktail boat” Int. Comp. Biol. 54 969-973 (2014). Right: Bryant Kelly Flickr (CC BY 2.0).
Graduate Research Assistants: Mark Brant, Patrick Bishop
Research Interns:
- Daniel Horvath
- Max Werkheiser