During Spring 2016 MEGL ran a program with 23 participants. There were five research groups (named Orbits, Special Words, Polytopes, Allen-Cahn Equation, and Embedded Graphs), two visualization groups (named 3D Printing and Virtual Reality), and one public outreach group, simply named Outreach. The research and visualization groups engaged in experimental exploration involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, make conjectures from data, and work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and libraries. The Spring semester ended with a Symposium where all teams presented their work.
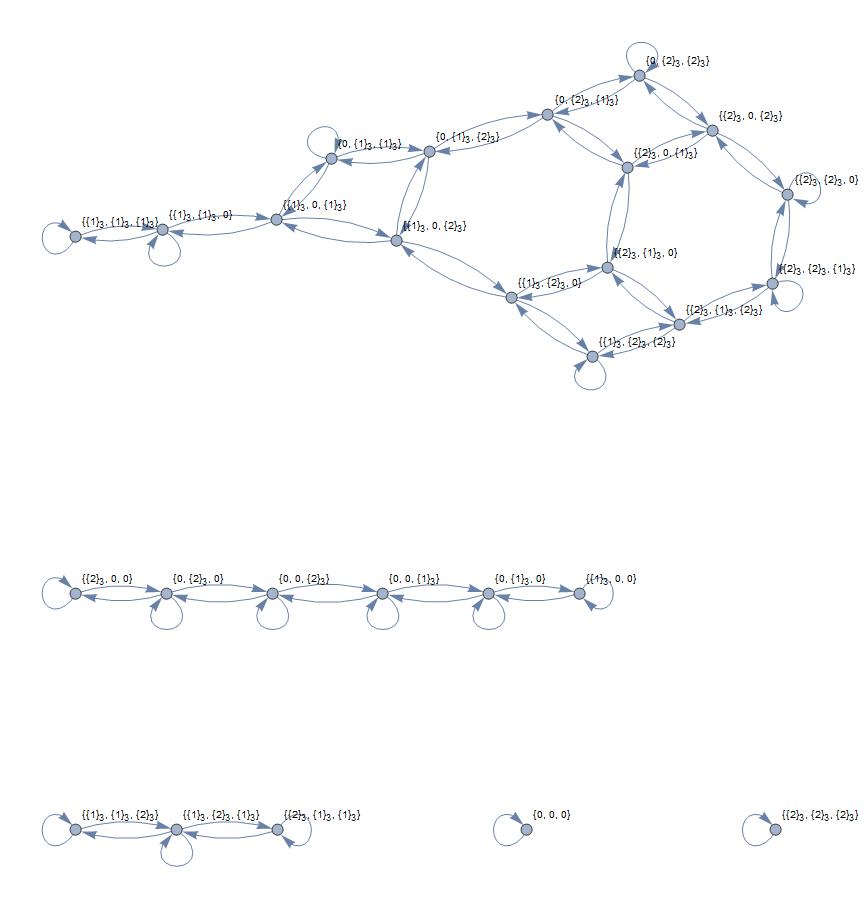
We are trying to understand the dynamics of the action of the outer automorphism group of a free group of rank $r$, denoted $Out(F_r)$, on the finite field points of the $\mathrm{SL}_2(\mathbb{C})$- character variety of a free group. One of the questions involve finding an upper bound for the length of the largest orbit under this action for a fixed element of $Out(F_r)$.
From previous computations, we know the upper bounds when the rank of the free group is two. The next question is to figure out if there are elements of $Out(F_r)$ such that the length of the orbit equals the given bound. Eventually, we would like to find out the growth of the length of the largest orbit as the rank of the free group and the order of the finite field varies. This work will continue into Summer 2016.
A word is an element of a rank 2 free group. The function that gives the trace of a word is the trace of the resulting matrix when the letters in a word are replaced with determinant one matrices. We define a words as special if they have the same trace function and are not cyclically equivalent. Words are 2-special if 2×2 matrices are used and 3-special if 3×3 matrices are used. Previously, we have proven that a word will be 2-special with its reverse, inverse, and inverse of reverse, but will never be 3-special with its inverse.
This semester we have proven that in order for words to be 3-special they must have the same exponents, indicating that a word cannot be 3-special with its inverse of reverse except in a case we call the alpha symmetric locus. We developed a computer program to search this locus for 3-special words. We conjecture that a word will not be 3-special with its reverse, and to explore this conjecture we wrote a computer program that constructs the Fricke polynomial for a word. We believe that by studying the structure of the Fricke polynomial we will be able to prove that a word is not 3-special with its reverse. It is unknown whether 3-special words exist, and this project is part of a larger project to determine their existence. The existence of 3-special words has consequences for geometry and representation theory.
A Lie group is a finite dimensional smooth manifold that is also a group with group operations that are smooth maps. Every Lie group has a corresponding underlying vector space and Lie bracket known as a Lie algebra. Our main focus of research during the 2016 Spring semester is to understand what $P_3(G)$ is and how to generate a Hilbert basis for it. Where $G$, here is a rank 2 lie group. This work will continue into summer 2016.
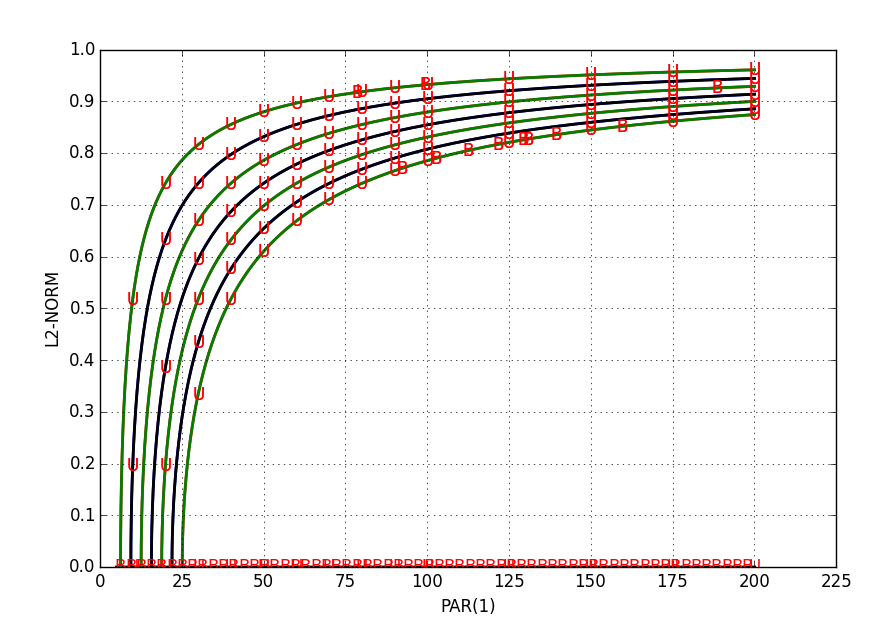
The Allen-Cahn equation is a partial differential equation that models the phase changes of certain chemical elements. To determine the areas where a phase change occurs, the stability and metastability of the equation needs to be investigated. Using MATLAB, initial plots of the bifurcation diagrams for the Allen-Cahn equation were created, which gave a basic notion of the approximate locations of the equilibrium points. Furthermore, AUTO, a computer software designed to investigate bifurcations, helps determine the exact bifurcation points in both 1D and 2D. Extending the model to 3D is the next step. From here, we are able to gain a deeper insight into the Allen-Cahn equation and its stability.
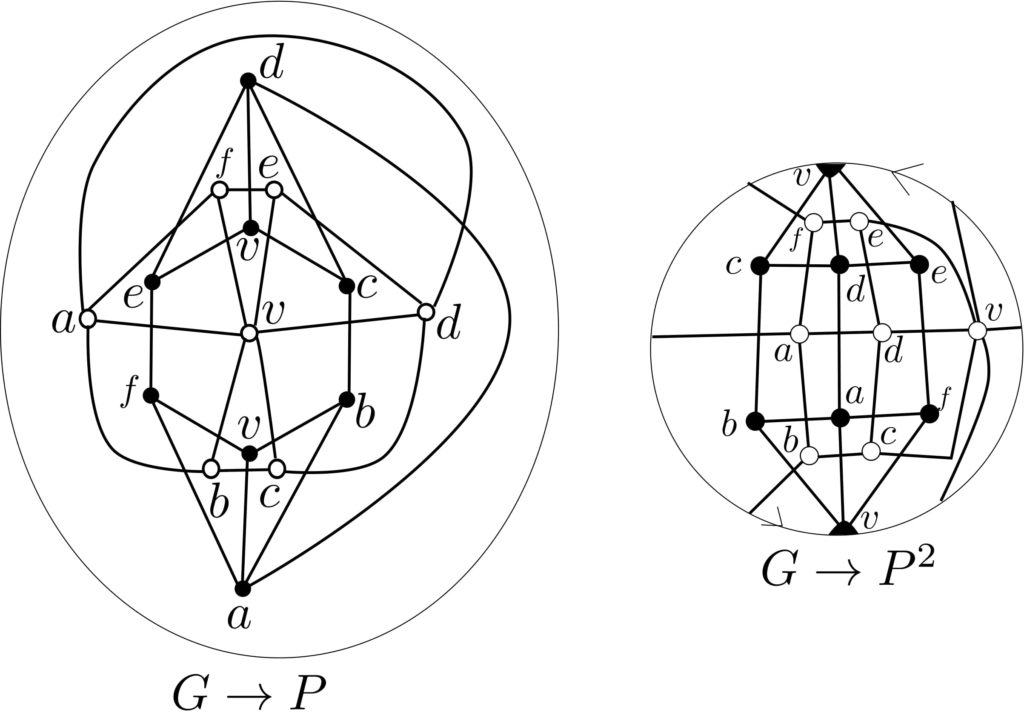
A proper embedding of a graph G in a pseudosurface P is an embedding that maps vertices of G to pinchpoints of P and induces a cellular decomposition of P. The dual graph of a proper embedding G → P captures the incidence of faces and edges of G → P, and we say that G → P is self dual if the dual graph is isomorphic to G. Using elementary argumentation, we can show that a connected graph must have at least 13 edges if it is possibly self-dual embeddable in a pseudosurface. With some combinatorial insight, and with the aid of a computer, we are working on determining the self dual embeddability of all connected graphs with 13 edges in pseudosurfaces. We are working on using multiprocessing to extend our results to connected graphs with 14 edges.

The Virtual Reality team worked on developing research and educational tools this semester. Early in the spring semester, we were visited by Dr. Daniel Ramras from IUPUI, (link to his website: [*http://math.iupui.edu/~dramras/ Dr. Ramras]), who asked us to visualize a set of rotations (elements of the group $SO(3)$) discussed in his paper, “How efficiently can one untangle a double twist? Waving is believing!”, link here: [*http://www.math.iupui.edu/~dramras/D-article.pdf Article] The paper discusses the mathematics behind the Filipino candle dance and the belt trick, and formalizes this nullhomotopy in $SO(3)$ by a set of parametric quaternion equations. We used these equations to create a virtual reality demonstration in Unity, where the user explores this nullhomotopy. The demo is not for the faint of stomach–the quaternion relations take you through every possible head position in $SO(3)$. The download for Mac and Windows can be found on the Visualization page.
During the second half of the semester, we were focused on visualizing the solutions to Ordinary Differential Equations (ODEs). A system of three ODEs gives a solution that can be visualized as a curve in flat 3D space. Our goal was to solve a set of ODEs for arbitrary initial conditions (the “beginning” of the curve), and dynamically create a curve that approximates the solution. In order to numerically approximate the solutions to the ODEs, we implemented a fourth-order Runge-Kutta (RK4) method in our code. RK4 uses the weighted average of four increments to approximate the next function value. Since it is significantly more accurate than Euler’s and possible to code in one line, RK4 was the most efficient choice for this visualization. Using this method, we numerically solved and visualized several nonlinear ODEs. Attractors such as the Lorenz attractor and the Aizawa attractor are able to be seen in our program. We are currently working on making a dart game based on the vector fields (the velocity of the dart) defined by the ODEs.
Going forward, we are going to work on the moduli spaces of polygons. A question we will tackle is that of whether or not it is possible to tell if these sets are convex or not, and if this is possible we will work on possible visualizations of these spaces.
Link to Visualizations Page

In the 1950’s, Nash and Kuiper proved the existence of an isometric embedding of a flat torus in 3D Euclidean space; however, they did not provide a visualization of such embedding. In the 70’s and 80’s, Gromov developed the convex integration technique, providing the tool for such construction. From 2006 to 2012, three French mathematics institutions collaborated in the HEVEA project to produce a 3D model of such embedding. Last semester, we developed a new construction inspired by the self-similarity and fractal structure of the HEVEA project solution. In this new technique, which we call the sinusoidal fractal, increasingly higher frequency sine waves were wrinkled normal to previous iterations, instead of corrugating along a single direction. We proved that this construction satisfies all three conditions for an isometric embedding from 1D to 2D. Utilizing sinusoidal fractal curves, we constructed a model of the isometric embedding of a flat torus in 3D and produced a physical visualization using a 3D printer.
One of the follow-on goals of the HEVEA Project was to develop a construction of the Nash-Kuiper sphere, which is an isometric embedding of a larger sphere onto a smaller sphere. This is a corollary that follows directly from the Nash-Kuiper theorem. In our attempt to provide a construction of such sphere, we corrugate sinusoidal fractals along the orthogonal azimuth and elevation directions of the smaller sphere. We proved that this construction satisfies all three conditions for an isometric embedding and produced a physical visualization with a 3D printer.

During Spring 2016 MEGL Outreach held 19 events at 8 locations in and around Fairfax, Virginia, attended by roughly 670 students. The locations included elementary schools, high schools, and public libraries, where students engaged with activities that aim to shift, broaden, and enlighten their perspectives on mathematics.
The events included Your Teachers Are Lying to You, where students learn that mathematical truths depend on context and we need only shift our context to make liars out of our teachers and textbooks, You Can Count on Monsters, where students learn prime decomposition by creating multi-headed creatures, and new for Spring 2016, Really BIG Numbers!, where students gain an intuition for the magnitude of numbers through a series of kinesthetic, artistic, and multimedia experiences.
Symposium Pictures












