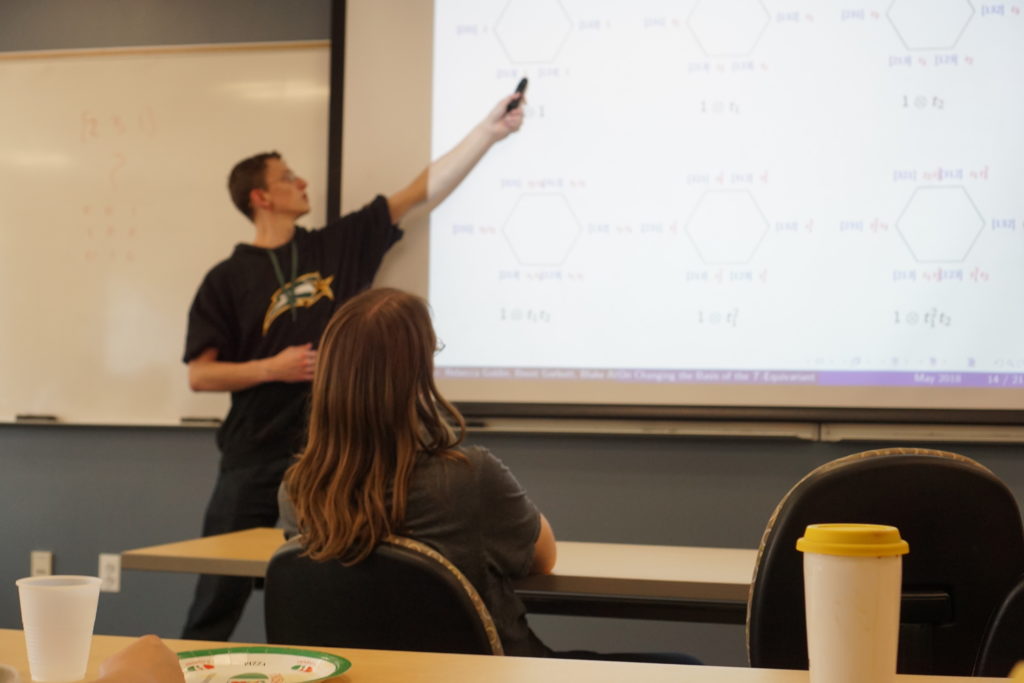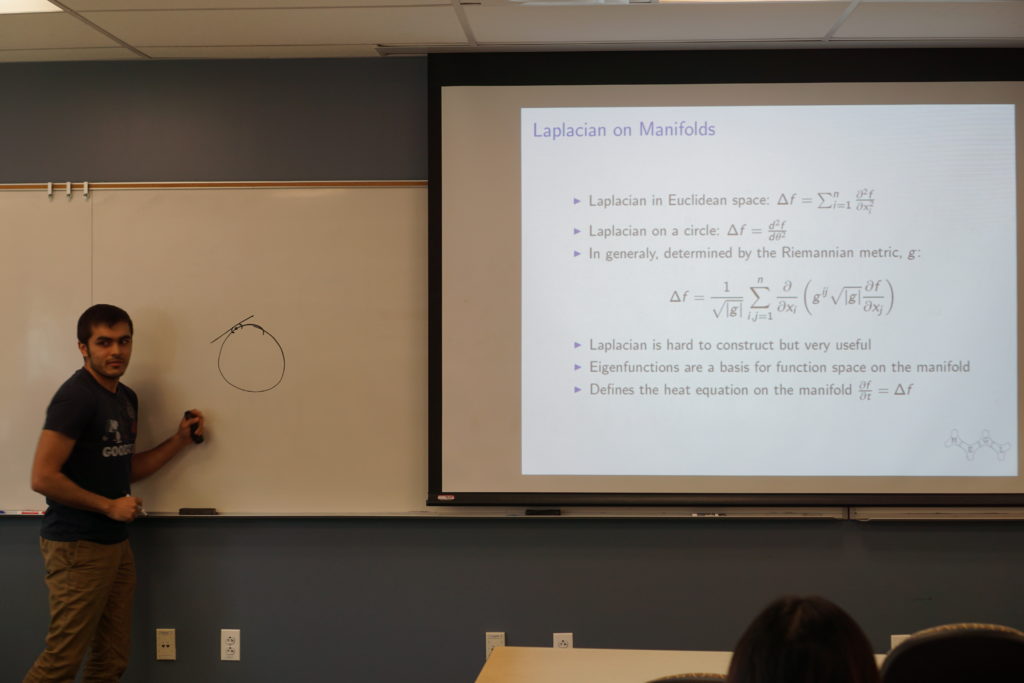During Spring 2018 MEGL ran a 6 project program with 19 participants (faculty, graduate, and undergraduate students). The five research/visualization groups were titled: Visualizing Continued Fractions, Asymptotic Dynamics on Arithmetic Curves, Applications of Diffusion Maps, Riemann Hilbert Correspondence in Categorical Language, and Equivariant K-theory of Flag Varieties. Additionally, there was one public engagement group which we refer to below as Outreach. The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries. We concluded with an end of term symposium and a poster session (scroll down for pictures).

It is standard to write numbers as a sequence of decimals, such as $\sqrt{2}=1.41421…$ Another way to write a number is to specify a sequence of descending continued fractions that represent it. In this way, we can write $\sqrt{2}=1\frac{1}{2+\frac{1}{2+\frac{1}{…}}}$. This idea can then be extended to complex numbers as well. The goal of this project was to visualize continued fractions and explore the relationship between two natural equivalence relations on continued fractions: tail equivalence and matrix equivalence.

Two complex numbers $x$ and $y$ are said to be matrix equivalent if there exist Gaussian integers $a$, $b$, $c$, and $d$ such that $x=\frac{ay+b}{cy+d}$ and $ad-bc=\pm 1$. Two complex numbers $x=a_0+\frac{1}{a_1+\frac{1}{a_2+\frac{1}{…}}}$ and $y=b_0+\frac{1}{b_1+\frac{1}{b_2+\frac{1}{…}}}$ are said to be tail equivalent if there exist positive integers $r$ and $s$ such that $a_{n+r}=b_{n+s}$ for all positive integers $n$. In other words, $x$ and $y$ are tail equivalent if there is a way to align their continued fraction digits so that their tails match. It can be shown that two real numbers are matrix equivalent if and only if they are tail equivalent. For complex numbers, however, tail equivalence implies matrix equivalence, but there exist exceptions to the converse. Previously, the only known example of matrix equivalent numbers which are not tail equivalent was given by Richard Lakein (1974). In this project, we successfully found more such examples.

We investigated the dynamics of the group action on affine 3-space induced by $\Gamma = \mathrm{Out}(F_2) = \langle \eta, \tau, \iota \rangle$.
In particular, we explored definitions of measure on $\kappa$ varieties in affine 3-space over finite fields in which we believe this action to be ergodic.
We discovered that the induced action of $\Gamma$ on the variety is equivalent to the group generated by $\langle \eta, \tau \rangle$, since $\iota = \tau\eta\tau\eta^{-1} \tau\eta $.
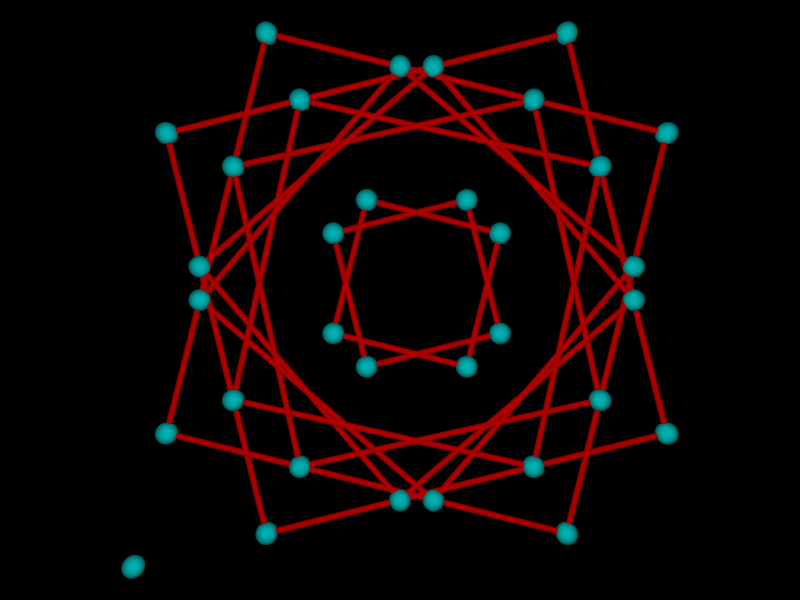
We developed the Exceptional Orbit Conjecture, which classifies our group action into seven different orbits, six of which are fixed and finite for all prime $p$.
The remaining elements form a single orbit, which is the maximum orbit on which the action is transitive.
The computational data strongly supports this, and if proven, the Exceptional Orbit Conjecture implies the ergodicity of this action.
Fun encounters include: requiring the affirmation of the Riemann Hypothesis for a bound of interest and orders of elements relating to the solution of Pisano Periods.
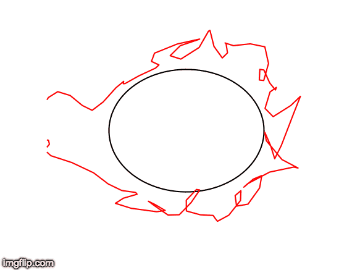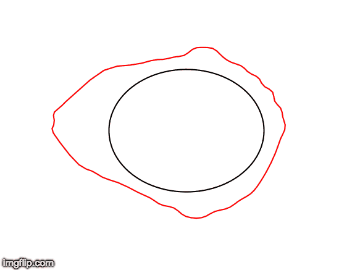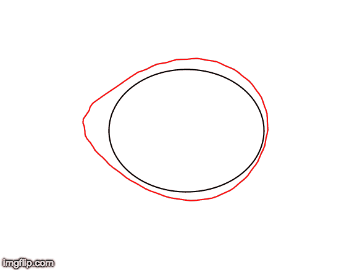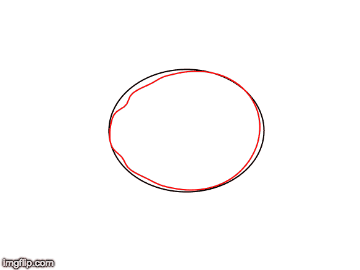
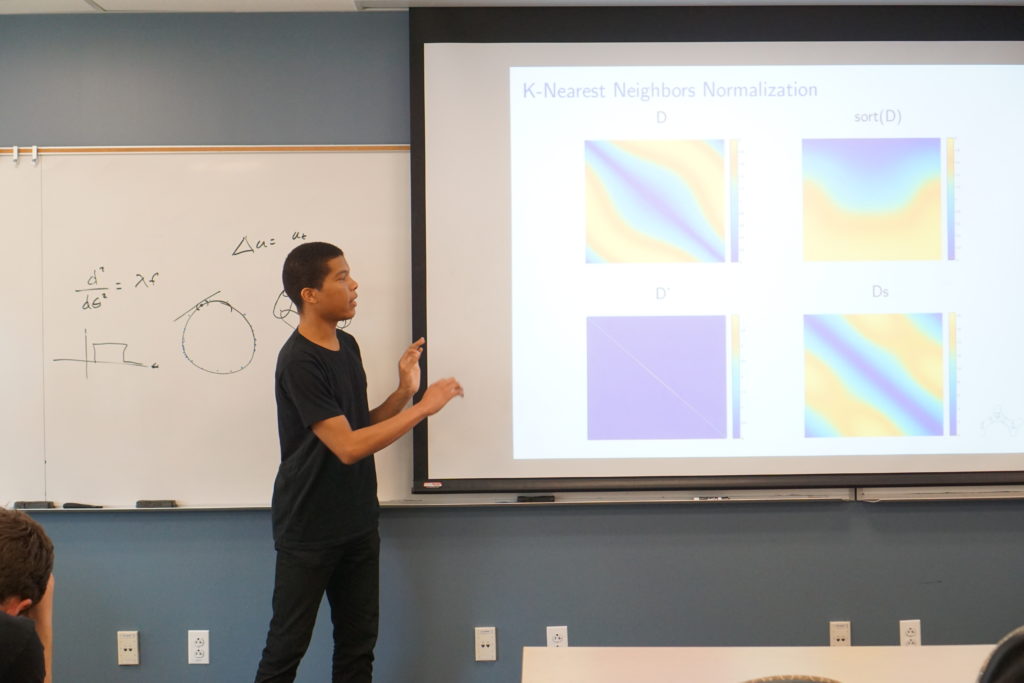
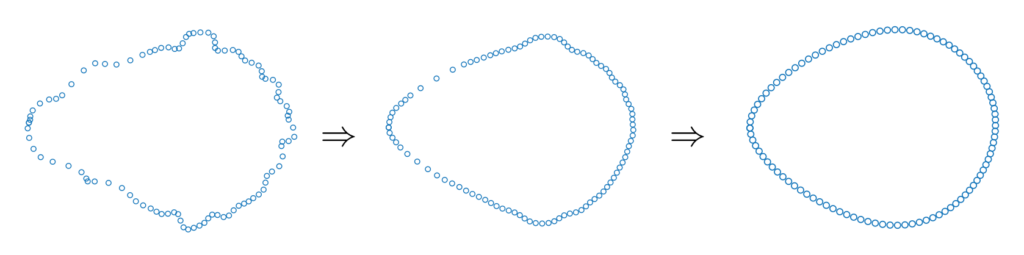
This semester the main goal of the geometric flows team was to solve the long term instability we had discovered in our simulations of the geometric heat flow. We started by simulating the geometric heat flow on the unit circle, which should be invariant under the flow. Simulating the flow using a uniform grid of points on the circle, we found that after many steps the symmetry of the grid would break and the data points would collapse onto each other. We hypothesized that we could stabilize the flow by resampling the data points to maintain perfect symmetry at each step of the solver.
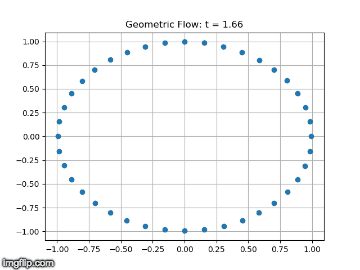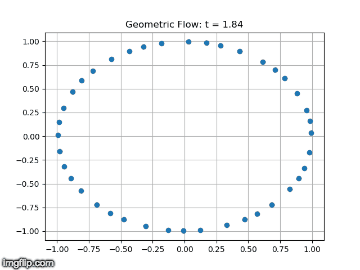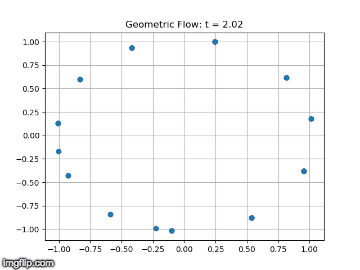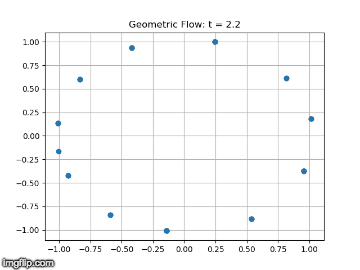
In order to resample the data points to maintain the symmetry, we planned to use the fact that the diffusion map construction of the Laplacian is invariant of the sampling of the data points. This theoretic fact suggested that if we could `invert’ the diffusion map, the resulting data points would be uniformly sampled, implying a symmetric grid. We tried several methods of inverting the diffusion map explicitly, but these led to distortions of the geometry. Finally, we had success inverting the diffusion map implicitly as a linear combination of the diffusion map eigenfunctions. This representation suggested that we could also simplify the embedding of the data while maintaining the geometry. We developed a gradient descent optimization scheme to reduce the dimensionality of the embedding while maintaining the geometry.
In the context of algebraic topology, being able to characterize covering spaces over a topological space $M$ leads to interesting topological and algebraic questions. Say the space $M$ is a smooth connected manifold with specified basepoint $x\in M$ and good cover $ (U_{\alpha} \to M)_{\alpha \in A}$, then we can identify the category of covering spaces $Cov/M$ with a functor category $\text{Fun}(\Pi_1(M),\text{Set})$. This is advantageous because functor categories are quite convenient. Say $M$ is a connected manifold and we wanted to characterize a different structure “over” it; we would like to give an algebraic description in terms of a functor from the fundamental groupoid to the category of finite dimensional vector spaces. It turns out this this is in effect the assignment of a vector bundle over $M$, with flat connection on the bundle. The Riemann-Hilbert correspondence states that this is due to an equivalence of categories between local systems of vector spaces over $M$ and flat vector bundles over $M$.
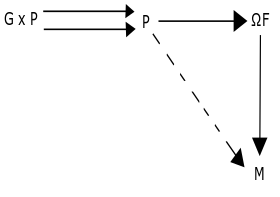
We can create a functor $\Omega : \text{Fun}(\Pi_1(M),\text{Vect}{\mathbb{R}}^{f.d.}) \to \text{Bun}{\flat}(\text{Vect}{\mathbb{R}}^{f.d.},M)$ where the target category is the category of flat vector bundles over $M$ and vector bundle homomorphisms that preserve the connection through pullback. To each functor $F:\text{Vect}{\mathbb{R}}^{f.d.}$, we assign the vector bundle $\Omega F \to M$ associated to the principal bundle $\tilde{M} \to M$ (defined by the functor $\text{Hom}{\Pi_1(M)}(x,-):\Pi_1(M) \to \text{Set}$) and representation $F|x:\pi_1(M,x) \to \text{Aut}(Fx)$. To each natural transformation $\alpha$ we assign the map induced by the intertwining map $\alpha_x$. Going the other direction, to each vector bundle with flat connection $E$ we can extract the corresponding parallel transport as a functor $\Lambda E: \Pi_1(M) \to \text{Vect}{\mathbb{R}}^{f.d.} $. To each morphism $\phi$, the component of the corresponding natural transformation at $y$ would just be the restriction of $\phi$ to $y$, and naturality corresponds to the maps being “equivariant” with respect to the transport. These functors are inverses of each other up to natural isomorphism, and so define an equivalence $\text{Fun}(\Pi_1(M),\text{Vect}_{\mathbb{R}}^{f.d.})$. This gives a characterization of flat vector bundles akin to that of covering spaces.
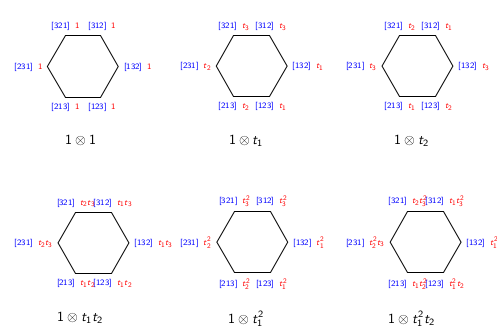
The flag variety $G/B$ has an action by a maximal torus $T$ of $G$, by left multiplication. This action allows us to consider the Grothendieck ring of $T$-equivariant vector bundles on $G/B$, called the equivariant $K$-theory of $G/B$, and denoted $K_T(G/B)$. In the case that $G/B$ consists of the set of flags in $\Bbb{C}^3$, we considered two different bases of this ring as a module over the equivariant $K$-theory of a point. One of these bases is represented by line bundles, while the other basis is represented by structure sheaves on the Schubert varieties. Our goal was to find an explicit change of basis. As a tool, we began the development of a program in Python to carry out some of the calculation. We successfully expressed each dual line bundle in the basis of line bundles, as well as several of the Schubert varieties.

This spring MEGL Outreach continued our upward trajectory, presenting 29 outreach events to over 700 students. We are also maintaining our goal of developing one new activity each academic year. This Spring we created //Playground of the Infinite,// which is intended to be a sequel to //Really Big Numbers//, but is also designed to stand on its own. In this activity students explore some of the strangeness of infinity, and discover that there are infinitely many different sizes of infinity.
In administrative news, starting in Fall 2018 MEGL will have a faculty position in the math department devoted part time to directing our outreach program. This means we have more resources for the development, implementation, and expansion of MEGL Outreach, so that the growth we have experienced since our inception in 2015 will not only be maintained but accelerated.
We thank Stephen Liddle (Fall 17-Spring 18) and Akhila Dasar (Spring 18) for helping the outreach team!