During Fall 2021 MEGL ran a 4 project program along with aiding 3 honor thesis projects with 23 participants (faculty, graduate, and undergraduate students). The four research/visualization groups are titled:
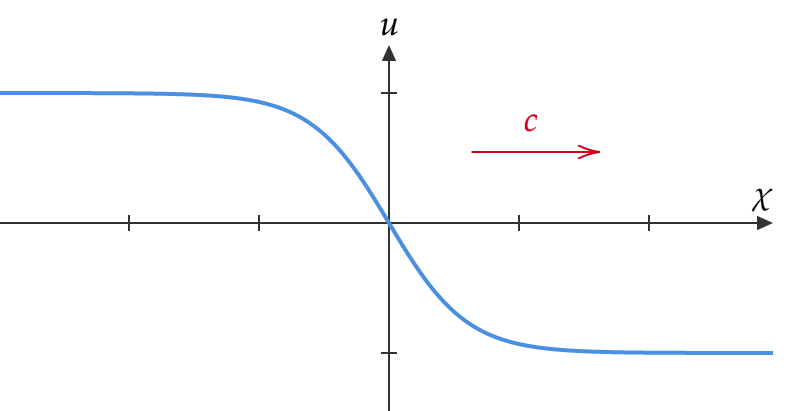
- The stability of icebergs and other floating objects
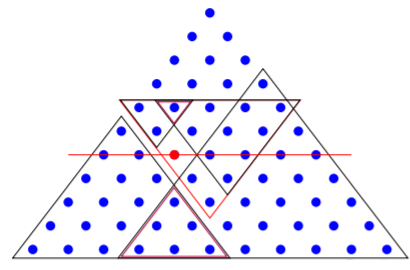
- Cores and hulls of ideals of commutative rings
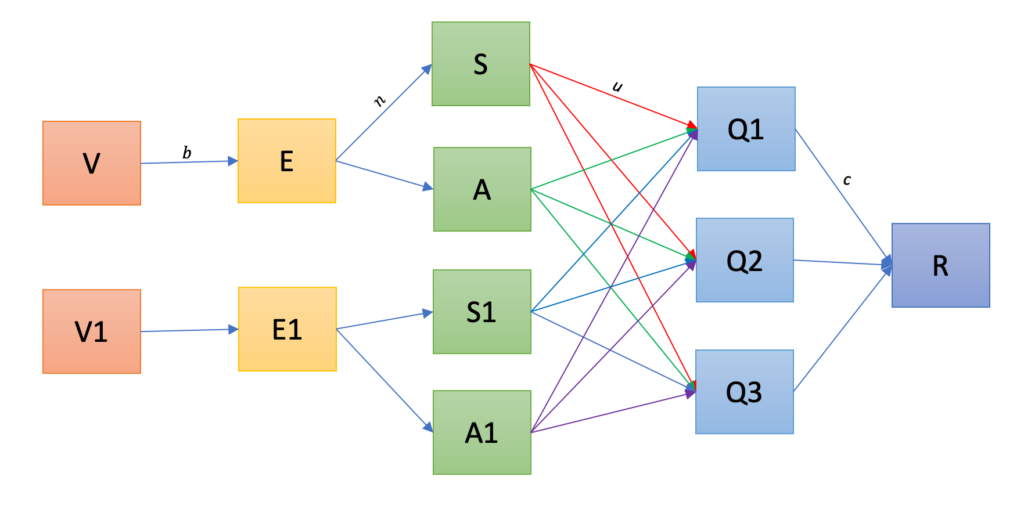
- Mathematical modeling, analysis and control for understanding the spread of infectious diseases
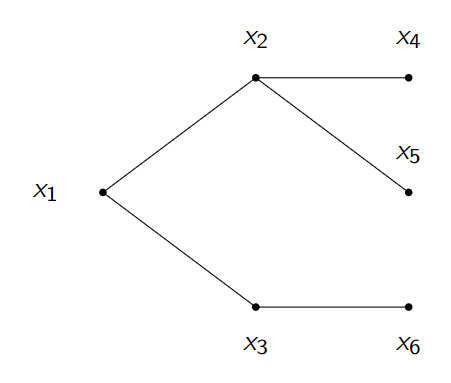
- Combinatorics of cohomology rings of Peterson varieties
The three honor thesis projects are titled:
- Speed and stability of traveling waves in population growth models
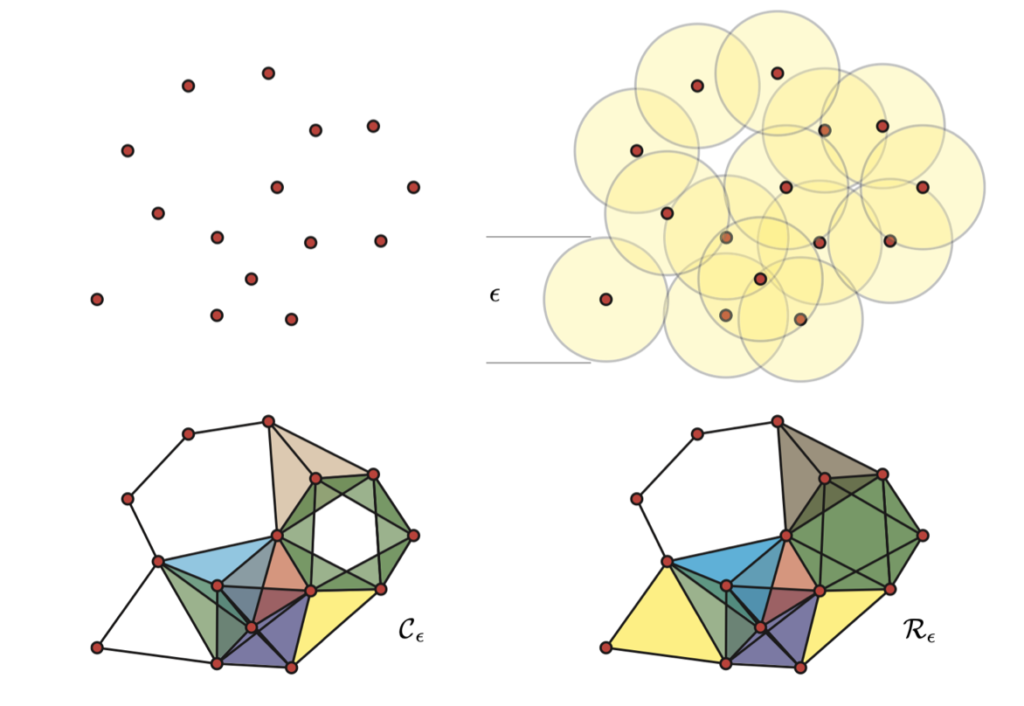
- Persistent homology
- Vertex algebras
In addition to these projects, MEGL ran a public engagement group which we refer to below as Outreach.
The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries.
We concluded with an end of term symposium and a poster session, sharing progress and results of our research. To learn more, see below:
Faculty Mentor: Professor Daniel Anderson
Undergraduate Research Assistants:
- Lujain Nsair
- Joshua Calvano
- Brandon Barreto
Analyzing the stability of floating objects via quantities like the center of mass, the center of buoyancy, and the metacenter. Our goal was to analyze the relationship between shapes, mass distributions, and buoyant forces to predict the stability and favorable floating orientations of shapes with simple and complex geometries using numerical and analytical approaches. We designed a Matlab code to test our hypothesis and were able to confirm the necessary and sufficient conditions in the equilibrium of a floating body, and discovered unique properties of special 2D geometrical objects such as; circles, squares, and rectangles. Using the property that a system in stable equilibrium has a minimum value of potential energy, we implemented a formula that is useful in determining the stability of an object as well as in graphing potential energy landscapes. It is found that a floating body is in stable equilibrium if its center of gravity has a minimum height with respect to its related center of buoyancy.
Faculty Mentor: Professor Rebecca R.G.
Graduate Research Assistant: John Kent
Undergraduate Research Assistants:
- George Andrews
- Aiden Donahue
The integral core of an ideal of a commutative ring is used to Stanley-Reisner rings are a class of commutative rings with associated simplicial complexes. Using results from a 2021 paper by Vassilev on tight interiors, we computed many examples of tight interiors for ideals of Stanley-Reisner rings by looking at the structure of these complexes and their associated rings. We studied the effect augmenting the complex had on corresponding ideal interiors and hulls. We found formulas which indicate the way an ideal’s interior change when the original complex has more simplices added to it.
Faculty Mentor: Professor Padhu Seshaiyer
Undergraduate Research Assistants:
- Clarissa Benitez
- Krista Cimbalista
- Jolypich Pek
- Raina Saha
This research project develops mathematical models that characterize the spread of COVID-19 on the GMU campus. It is based on the SEIAQR epidemic model and focuses on the unique situation at George Mason. We take into account the effects of the university’s preventative measures by analyzing extensions of the SEIAQR model and their reproduction numbers. From this, we can determine how effective the university’s guidelines are and better understand the transmission of COVID-19 for this type of environment.
Faculty Mentor: Professor Rebecca Goldin
Undergraduate Research Assistants:
- Swan Klein
- Connor Mooney
Our goal was to verify a conjecture about the decomposition of the restriction of Schubert classes associated with transpositions to the Peterson variety into a linear combination of Peterson classes. Using a corollary to Billey’s formula, we reduced the conjecture to a more concise combinatorial question about counting reduced words for transpositions embedded into long words. We uncovered an elegant visual framework for understanding these combinatorial questions. Future work will involve simplifying the expressions we obtained, evaluating whether they confirm or contradict the prior conjecture, and extending our combinatorial strategy to as many types of Schubert classes as possible.
Faculty Mentor: Professor Harrison Bray
Graduate Assistant: Aleyah Dawkins
Undergraduate Assistants:
- Aidan Donahue
- Lujain Nsair
- Susan Tarabulsi
This semester, we reached 659 students. We were able to run 34 activities, reaching students from grade levels K-6 from 9 different organizations. This semester we were able to continue running virtual-hybrid events, while also returning to in-person events. We focused on the activities “You Can Count on Monsters”, “Really Big Numbers”, and “Your Teachers are Lying to You”. Check out our website for more information on MEGL outreach activities.
Faculty Mentor: Professor Matt Holzer
Undergraduate Research Assistant:
- Zach Richey
We expand upon the Fisher-KPP equation by introducing a nonlocal diffusion term in the form of a convolution operator. We study the stability of travelling wave fronts that arise as solutions to this equation. Viewing these solutions as equilibria in a moving reference frame, we use techniques including perturbation methods, Laplace analysis, and exponentially weighted spaces to study their linear and nonlinear stability.
Faculty Mentor: Professor Sean Lawton
Undergrad Research Assistant:
- Shrunal Pothagoni
The purpose of data mining is to use advanced mathematical and statistical techniques to extract quantitative information from large data sets. These tools are incredibly powerful and in conjunction with machine learning algorithms allow for extremely accurate pattern prediction. However, there are various datasets that have qualitative properties that cannot be discerned using classic data mining techniques. Topological Data Analysis (TDA) is a recently developed field that uses methods in topology to extract these qualitative features. The goal is to study the use of abstract simplical complex on point cloud data sets to study their geometry using computational homology.
Faculty Mentor: Professor Sean Lawton
Undergrad Research Assistant:
- George Andrews
Vertex operator algebras provide an algebraic way to formalize quantum field theories. More Vertex operator algebras provide an algebraic way to formalize quantum field theories. My goal was to construct the vertex operator algebra associated with the affine Lie algebra corresponding to SL_2(C). I started by looking for simpler examples of vertex operator algebras, and along the way found classifications for finite dimensional vertex operator algebras over C and their modules.