During Fall 2018 MEGL ran a 7 project program with 24 participants (faculty, graduate, and undergraduate students). The six research/visualization groups were titled: Attacking Problems in Discrete Geometry using Satisfiability Solvers, Arithmetic Dynamics on Moduli, Geometry of Complex Networks, Geometric Flows and Dimension Reduction, Cooperative Parking for Self-Driving Cars and Equivariant K-theory of Flag Varieties. Additionally, there was one public engagement group which we refer to below as Outreach. The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries. We concluded with an end of term symposium and a poster session (scroll down for pictures).
This project involved using a computer program known as a satisfiability solver to look at a specific type of problem in discrete geometry. We wanted to find the smallest number $ N_d(n) $ so that $ N_d(n) $ points in general position in $ \mathbb{R}^d $ contain $ n $ points in convex position. For example, it takes 5 points in general position in two dimensional space to guarantee that 4 of the points form the vertices of a convex quadrilateral, and we were able to verify this with our satisfiability solver.
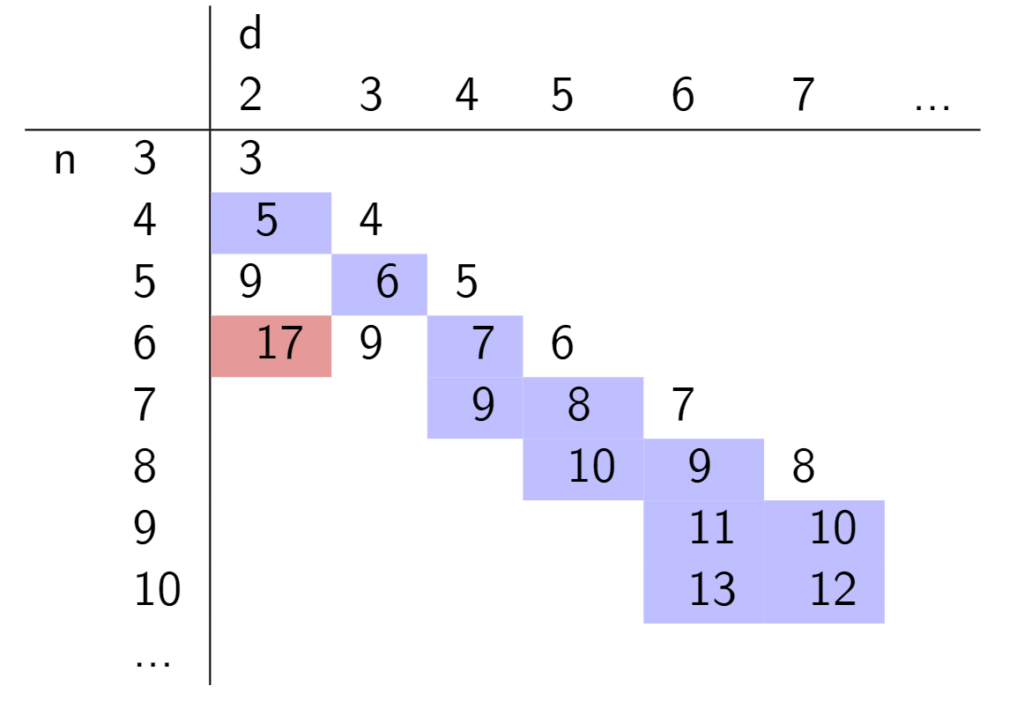
Chirotopes played a very important role in this project. A chirotope realized by a set of points $ E = {e_1,e_2,…,e_k} $ is a function χ mapping the set of ordered $ (d+1) $ element subsets of E to the set $ {−1,1} $. The values of the χ functions help determine the orientation of the set of points in d dimensional space. Combining our knowledge of chirotopes with our satisfiability solver, we attempted to determine how many points in three dimensional space are required to guarantee that 6 of the points form the vertices of a cyclic polytope. We found counterexamples with sets of 9 and 10 points. However, compuations are still running to see if every set of 11 points in general position in three dimensional space contains 6 points that form the vertices of a cyclic polytope.

Let $\mathfrak{X}_q^\lambda$ be the set of zeros in $\mathbb{F}_q^3$ of the polynomial $\kappa(x,y,z)=x^2+y^2+z^2-xyz-2-\lambda$ where $\mathbb{F}_q$ is the finite field of order $q$, $q$ is the power of a prime, and $\lambda$ is a fixed parameter in $\mathfrak{X}_q^\lambda$, we explored how the group generated by these three automorphisms, $\Gamma$, acted on $\mathfrak{X}_q^\lambda$. More specifically, we explored how the sizes of the orbits induced by this action compare to the size of $\mathfrak{X}_q^\lambda$.
We believe that the group action is almost transitive on $\mathfrak{X}_q^\lambda$ for most values of $\lambda$. That is, if $\text{Orb}(v)$ is the orbit of an element $v\in\mathfrak{X}_q^\lambda$, we expect $\frac{\max{\vert \text{Orb}(v)\vert:v\in\mathfrak{X}_q^\lambda}}{\vert \mathfrak{X}_q^\lambda\vert}$ approaches $1$ as $q$ goes to infinity. We approached this problem primarily using the method of conics by fixing one of the coordinates.
Bourgain, Gamburd, and Sarnak explored a similar problem using conics. By extrapolating their results, we were able to conclude that $\Gamma$ does act almost transitively on $\mathfrak{X}_q^\lambda$ in the case $\lambda=-2$ and $q$ is prime. We hope to generalize this result to other values of $\lambda$ if possible.
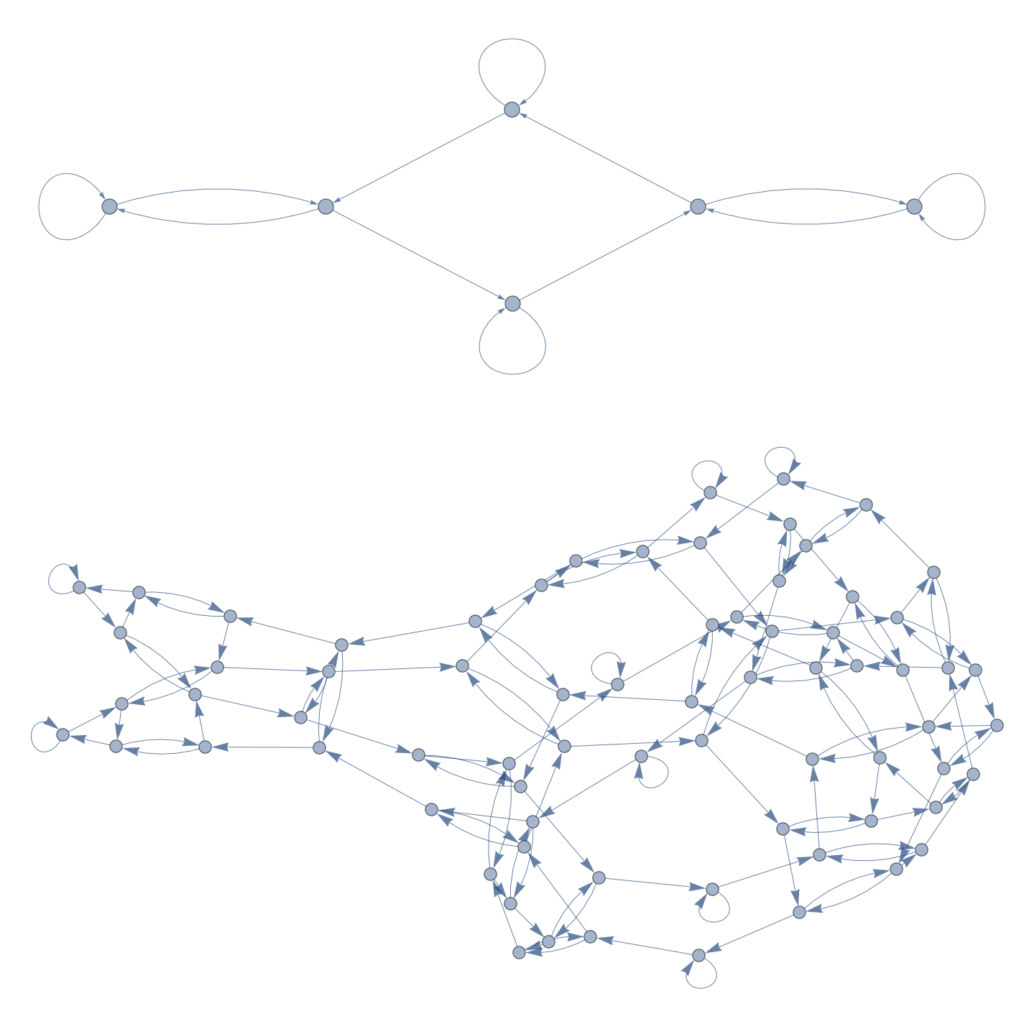
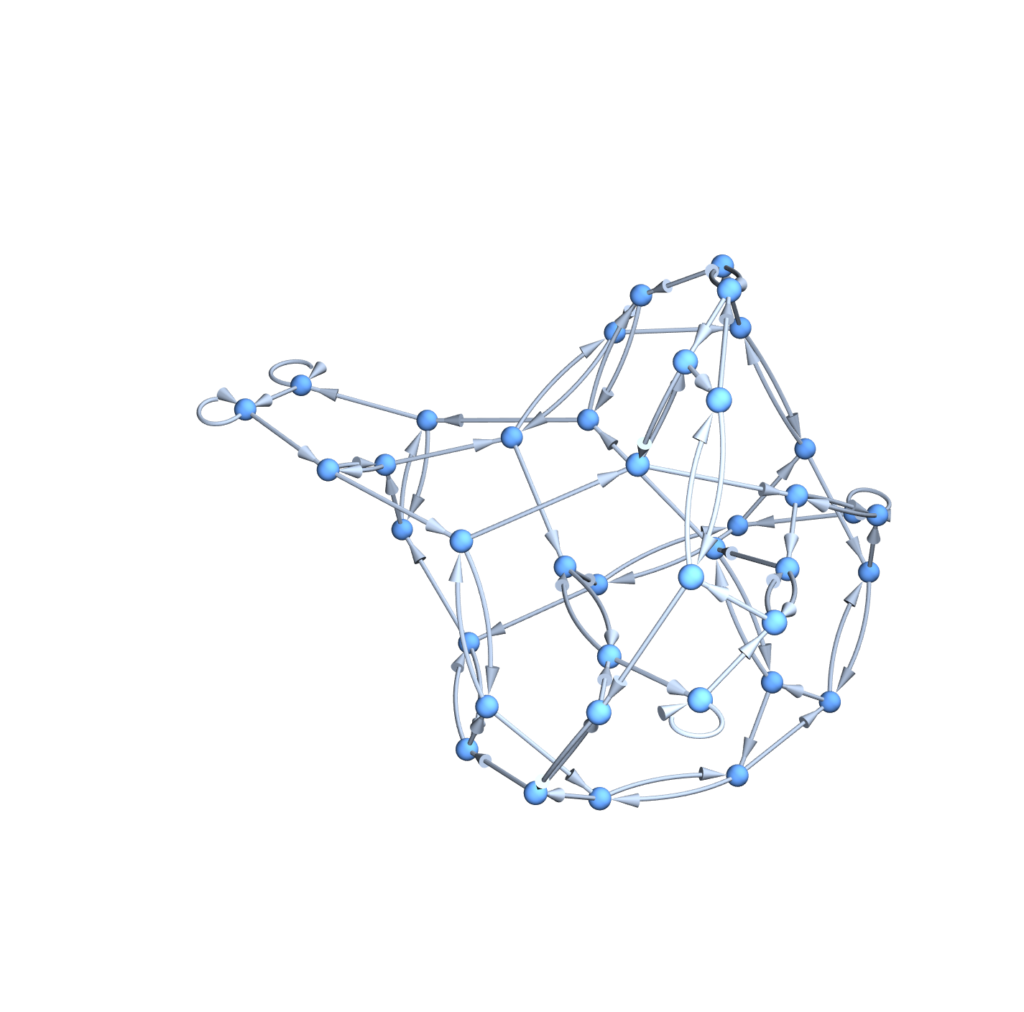
This semester the main goal of the determine the geometric properties of complex networks.
A network is graph, $ G = (V , E) $ with V vertices and E edges, and a complex network is a graph with non-trivial features that do not occur in simple networks such as lattices or random graphs but often occur in graphs modeling real systems. General features of real world networks: sparse, algebraic degree distribution (i.e. hubs exist), community structure, exponential growth of neighbors. In particular, we used the airline transportation network for our research.
Complex networks are too crowded to fit into Euclidean space, so we sought out to show that the network had hyperbolic properties. To measure hyperbolicity, we used the four-point condition to measure $\delta$-hyperbolicity. The closer $\delta$ is to 0 for a graph, the more hyperbolic a graph is.
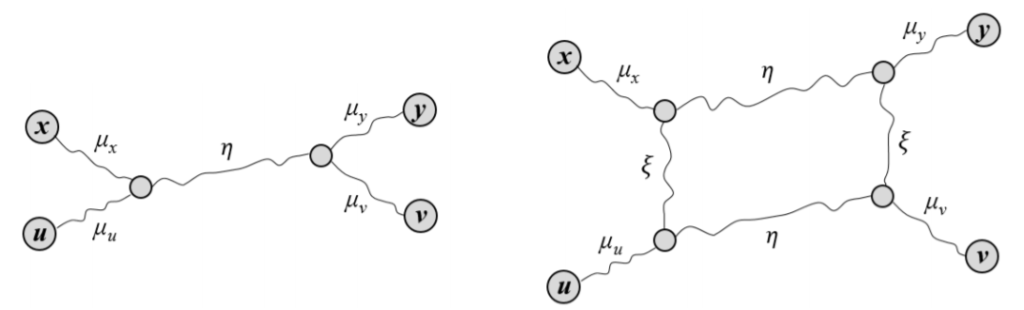
In a graph $G = (V,E)$, given four vertices $x$, $y$, $u$, and $v \in V$ with $d(x,y) + d(u,v) \geq d(x,u) + d(y,v) \geq d(x,v) + d(y,u)$, the hyperbolicity of the quadruple $x$, $y$, $u$, $v$ denoted as $\delta(x,y,u,v)$ is defined as:
$\delta(x, y, u, v) = \frac{d(x,y) + d(u,v) – (d(x,u) + d(y,v))}{2}$
The $\delta$ of a graph is the largest $\delta$ for all four point combinations. The $\delta$-hyperbolicity of the airline network is 1.5, compared to a diameter of 17, meaning that it is indeed very hyperbolic.
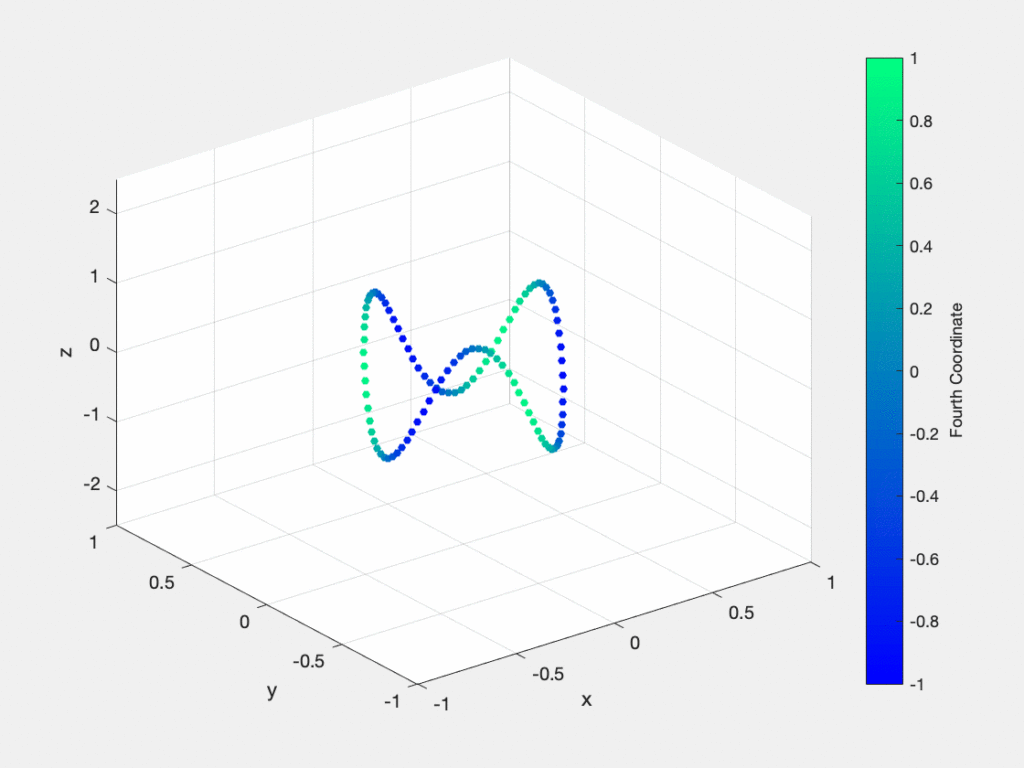
This semester the main goal of the geometric flows team was to further explore the possibility of using the Diffusion Map construction of the Laplacian for dimensionality reduction. We began by constructing this Laplacian from the data and parameterized our data with respect to the eigenvectors of the Laplacian. Our goal was to use these eigenvectors to construct a lower dimensional isometric embedding of the original data by choosing the appropriate Fourier coefficients. In other words, we sought to find a lower dimensional dataset with the same Laplacian as the original data. We attempted to achieve this optimization using a gradient descent, which was sped up drastically by calculating an analytic expression for the gradient. Additionally, we added a constraint to minimize the extrinsic curvature of the embedding. While this seemed to work, the gradient term alone wasn’t sufficient to minimize the Lagrangian for the constrained problem and we found that solutions tended to diverge. In future efforts we will try to add more constrains that will hopefully uniquely determine a minimal embedding for our data.
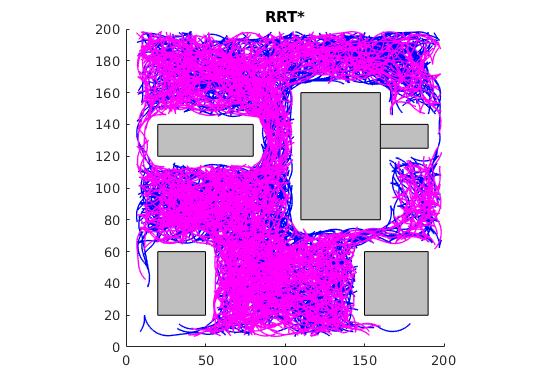
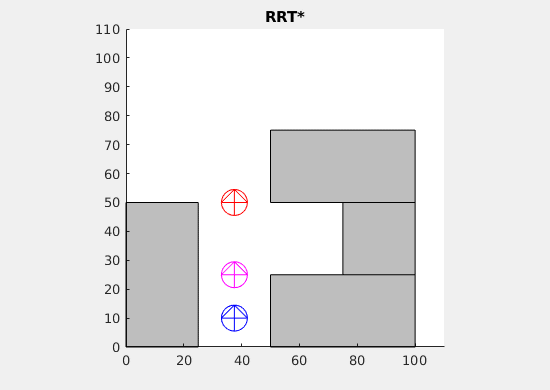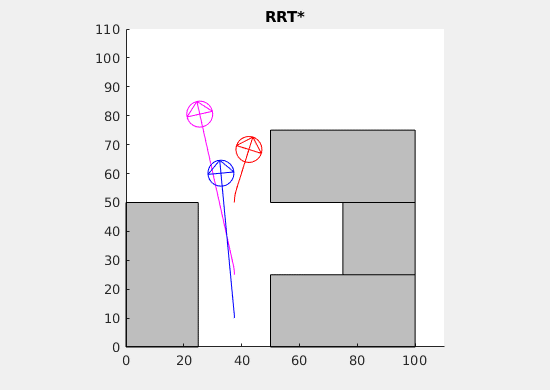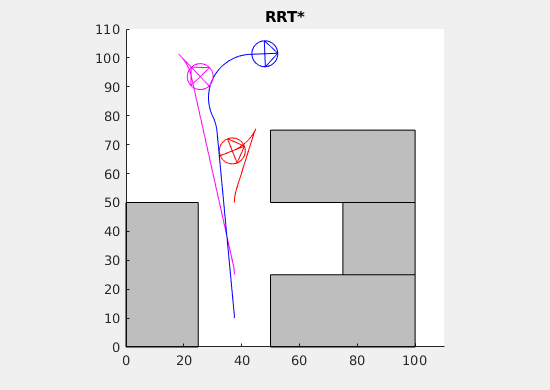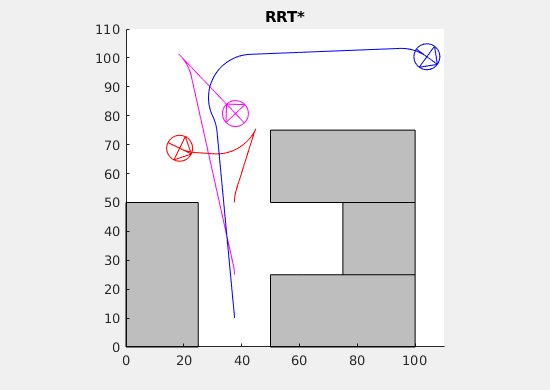
Self-Driving cars are quickly being integrated into society, but there are still lacking any motion-planning algorithms that effectively find paths for multiple cars. In our work, we aim to efficiently produce a motion-path that near-optimally choreographs multiple cars toward a specified location in our space. The purpose of designing this algorithm is to cooperatively park self-driving cars. On top of studying the properties of motion-planning algorithms with multiple cars, we also have developed simulations of the path-finding process and we have used the Mason Autonomous Robotics Lab’s Flock-bots in order to simulate this physically. On the algorithmic side, our team worked on extending the motion-planning algorithm RRT, Rapidly-Exploring Random Trees Star, to work with multiple cars while also retaining the algorithm’s inherent convergence properties. On the robotics side of the project, our team worked on taking the paths generated by the computational simulations of the multiple car RRT and using those to guide Flock-bot motion, effectively emulating self-driving cars.
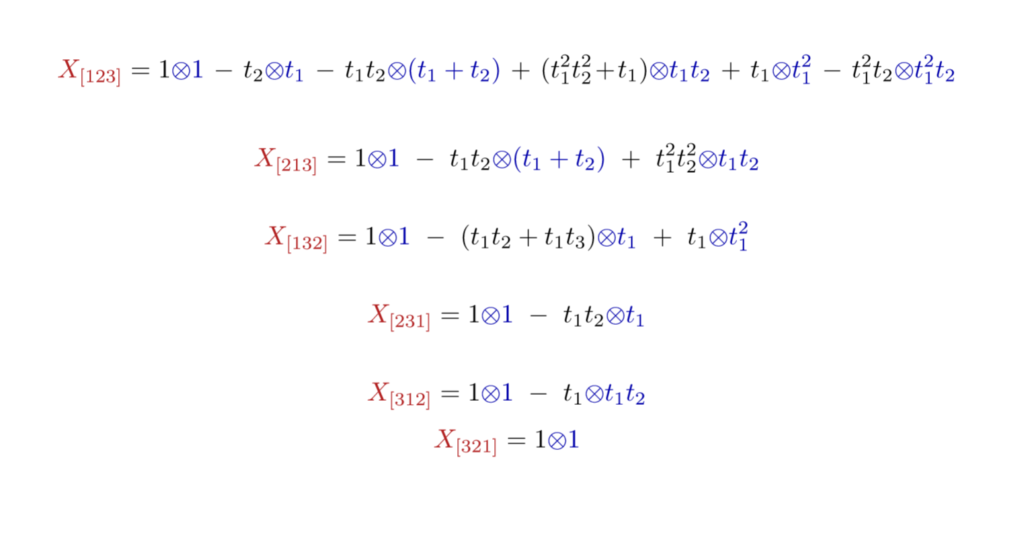
The group was primarily interested in working on the equivariant K-theory ring of $F = \textrm{Fl}(3,\mathbb C)$ with its effective torus action. We focused on this dimension to obtain methods that would translate to higher dimensions. This ring has a module structure over the representation ring of the torus, and there are two bases for it that were of interest to us.
The two bases are indexed by the symmetric group on 3 letters, $\mathfrak{S}3$ , and so there are 6 elements in each. The first basis, which we call the Line Bundle basis, consists of classes represented by the symbol $1\otimes \partial{\sigma} p$ where $p$ is $t_1^2 t_2$ and $\partial_{\sigma}$ is an operator determined by the permutation $\sigma\in \mathfrak{S}_3$. The second basis is of a more algebro geometric nature, and it is determined by the Schubert varieties that live inside of $F$.
Restricting classes to fixed points of the torus action gave us an injective ring map $K_T(F) \hookrightarrow \bigoplus_{\sigma \in \mathfrak{S}_3}R(T)$ where the sum is indexed over the symmetric group on 3 letters. This gave us a simplified way of looking at bases of the K-theory ring as a module, which meant we could apply linear algebra computations in SageMath to decompose one basis in terms of another. Our problem became describing each basis in terms of its restriction to fixed points. In dimension 3, we solved this, and our methods are manifestly generalizable to any dimension.

MEGL Outreach ran 17 events this semester, and our outreach activities have now been attended by over 5,000 students since 2015. In addition to our usual classroom-centered activities, we also took part in the George Mason University College of Science alumni open house and presented our work at the inaugural Women’s Intellectual Research Network Symposium (WINRS) held at University of Virginia. A parent of a high school student who took part in one of our activities shared the following feedback with their teacher:
[my child] came home after class COMPLETELY excited and had so much to tell me about how she felt like she was truly learning outside the box. It was challenging and she had to think outside her comfort zone. She absolutely loved it.