During Fall 2016 MEGL ran a program with 18 participants. There were four research groups (Orbits, Special Words, Polytopes, Embedding Graphs), three visualization groups (Geometric Surfaces, Virtual Reality, Double Pendulum), and one public outreach group (Outreach). The research and visualization groups engaged in experimental exploration involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries. We concluded with final reports from all teams and an end of term symposium.

We want to understand the dynamics of the action of the outer automorphism group of a free group of rank r, denoted $Out(F_{r})$, on the finite field points of the $SL_2(\mathbb{C})$ character variety of $F_r$ by looking at the length of the largest orbit. In particular, we are interested in elements of $Out(F_2)$ that exhibits a $p\text{log }p$ orbit growth as we increase the prime $p$ defining the finite field. We conjecture that the elements that shows this growth are pseudo-Anosov/hyperbolic elements and we try to get experimental evidence for small primes using Mathematica.
Another problem of interest is to define the notion of arithmetic ergodicity motivated from the definition in terms of measurable sets and use it to conjecture that for a compact surface $\Sigma$, $Out(\Sigma)$ acts arithmetically ergodically on the character variety $\mathfrak{X}_{\Sigma}(G)$, for all connected compact Lie groups $G$. Recent results by Bourgain, Gamburd and Sarnak have shown some light towards a special case which inspired the formulation of the conjecture.
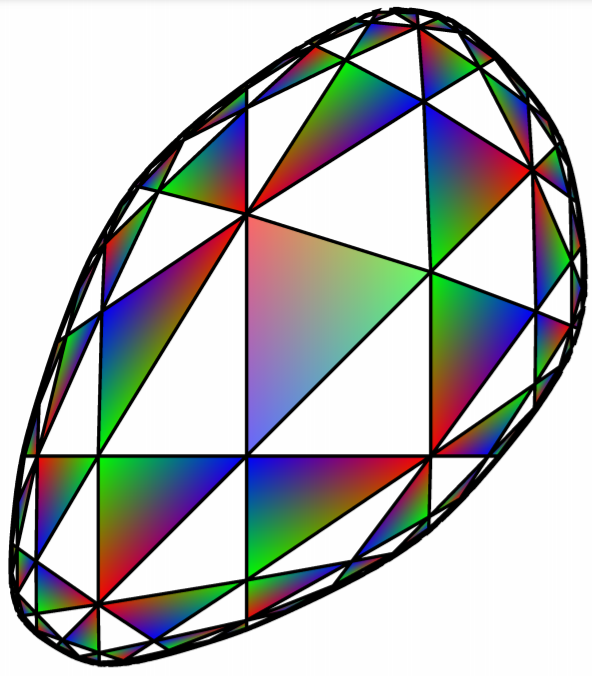
Words in the rank 2 free group are 3-special if they are not conjugate but have the same trace function. Two words are considered trace equivalent if they have the same trace for all choices of $SL(n,\mathbb{C})$ matrices. Words are considered 2-special if $SL(2,\mathbb{C})$ matrices are used, 3-special if $SL(3,\mathbb{C})$ matrices are used, etc. This research is to determine necessary conditions for words to be 3-special with the goal of determining if 3-special words exist at all. In previous work, we have determined algebraic obstructions for words to be 3-special. In the present work we search for geometric obstructions by studying bulging deformations. A bulging deformation is a deformation of a $\mathbb{R}P^2$-structure that is determined by an element of $SL(3,\mathbb{R})$. This semester we investigated bulging deformations by studying an example $\mathbb{R}P^2$ structure.
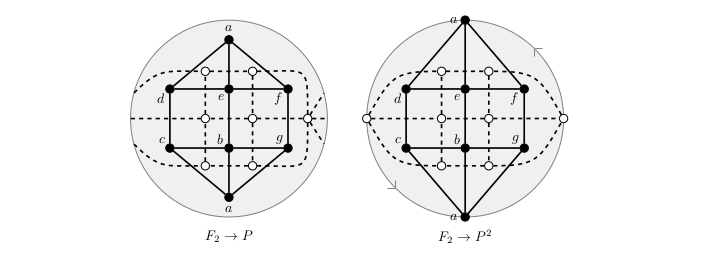
A proper embedding of a graph G in a pseudosurface P is an embedding in which the regions of the complement of G in P are homeomorphic to discs and pinchpoints of P correspond to vertices in G; we say that a proper embedding of G in P is self dual if there exists an isomorphism from G to its topological dual. We show that each graph that has a possibility of being self-dual embeddable in a pseudosurface must have at least thirteen edges, and we establish other criteria that such a graph must satisfy. We show that
there are five possible graphs that meet these criteria. Using the definition of an algebraic dual graph given by Abrams and Slilaty, we determine by way of computer-powered methods that exactly two of these five graphs are self- dual embeddable in the pinched sphere (the quotient of the sphere modulo the identification of two distinct points). We also utilize a surgery of Edmonds to produce self-dual embeddings of these graphs in the projective plane. We also determine that exactly one of the five graphs has a self-dual embedding in the projective plane and not in the pinched sphere.

The project was to display the idea of mathematics in motion. Therefore, the motion of the Double Pendulum was decided to be the 3D printed model as it displays chaotic motion, which is evident when the motion of the arm of the double pendulum is recorded and traced using the slow-motion feature of the camera application in the iPhone 7 in the case of this project. Since the double pendulum is composed of a simple pendulum with another simple pendulum hanging from its bob or arm, it is important to first understand the motion of the simple pendulum and the main equation that governs its motion and how such an equation is derived. Once we have learned the derivation of the equation of the simple pendulum’s motion, we can move on to see how the system of four differential equations for the double pendulum is derived through some simple trigonometric and physics problem solving methods and techniques. Applying these four equations and suitable values for the equations into MATLAB or capturing and recording the motion of the constructed 3D printed double pendulum results in a phase portrait of the pendulum’s motion and also allowed us to create a simulation of the traces of its motion in Mathematica. Other additional software used in the printing and modeling of the parts of the double pendulum including its vertical stand with a base, its two arms and some spacers include Makerware and OpenScad respectively. Some of the hardware that was used in assembling the 3D printed parts of the double pendulum were bearings to allow for a fluent motion of the double pendulum’s arms and some nuts and bolts.
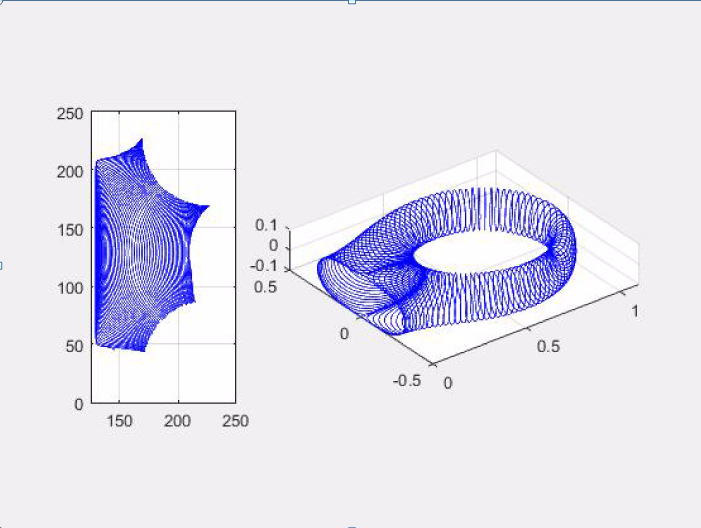
In the 1950’s, Nash and Kuiper proved existence of $C^1$ isometric embeddings (or immersions) of Riemannian manifolds into higher dimensional Euclidean space. Two decades later, Gromov invented the convex integration technique, providing the tool for the construction of $C^1$ isometric embeddings. From 2006 to 2012, three French mathematics institutions collaborated in the Hevea Project to produce a 3D model of an isometric embedding of a flat torus in 3D Euclidean space. In previous work, we formulated an alternative and simplified approach to constructing such an isometric embedding that is more easily adapted to other surfaces. One of our subsequent goals is to develop a construction of an isometric embedding of a hyperbolic double torus into 3D Euclidean space (parameterizd by a hyperbolic octogon). Before this isometric embedding could be achieved, it is first necessary to establish a corresponding parameterization. Furthermore, the parameterization must preserve angles between gridlines. In this talk, I will present corresponding parameterizations between a hyperbolic octogon and a doulbe torus using electric potential theory.

Our current project is making a Geogebra style geometry package that instead of being based on a Euclidean plane, is based on the flat torus. Even further, We are working to include functionality with the Oculus Rift, making this package a very immersive activity. Using the Unity Game Engine, we worked on stereo-graphically projecting the flat torus, as a subspace of the 3- sphere , into Euclidean 3-space. We also programmed an SO(4) action on the torus proper, which projected down onto the shadow of our torus. In parallel, we worked on how to import Euclidean geometry into a Unity scene, and we succeeded in making a working playground in which you can do Euclidean geometry on the plane.
In the Summer of 2016, the Polytopes group developed a program that interpreted trivalent pseudo graphs as relations between Berenstein-Zelevinsky (BZ) triangles and then calculated the Hilbert and Markov bases for the resulting polyhedral cones. During the fall of 2016, we’ve continued that work by tackling trivalent trees instead of the previous pseudo graphs. The leaf vertices were not implemented in our program as BZ triangles. Instead we considered two polyhedral cones for each tree, one in which the leaf vertices were considered ”free,” and one in which the leaf vertices are considered as a boundary term. The program made in the summer was amended to include these possibilities, and a table has been built to include the information gathered so far.

In the talk linked below, we give an overview of MEGL’s outreach efforts during the Fall 2016 semester. We give an idea of the philosophy of MEGL Outreach in general and give specific examples of how we are fulfilling it. These examples include descriptions of our activities, pictures from actual events, and the hard data of number of students and institutions reached during the semester. We also look at our plans for Spring 2017 and how we intend to keep MEGL Outreach growing.







