
During the Spring of 2023, MEGL ran a 6 project program with 38 participants between faculty, graduate, and undergraduate students. The six research/visualization groups are titled:
- Experimenting with Moduli Spaces
- Geometry Through Crochet
- Implementing the Polar Method
- Random 3D Polyforms
- Surfaces, Foliations, and Symmetry
- Surface Tension for Floating Objects
In addition to these projects, MEGL ran a public engagement group which we refer to below as Outreach.
The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries.
We concluded with an end of term symposium and a poster session, sharing progress and results of our research. To learn more, see below:
Faculty Mentor: Professor Sean Lawton
Description: In Spring 2023, we continued to study the dynamical system induced by the classical action of the general linear group over polynomials of arbitrary degree and number of variables in a finite field. We applied the results about invariants from Leonard Dickson to the problem of counting the number of fixed points, and tried to find closed form function for it. We did for the two variable case, and concluded that there likely isn’t one for a general number of variables. Using results we obtained last semester, we found conditions for full orbits, transitivity, and asymptotic transitivity. In particular, we found a non-trivial case of a space that is asymptotically transitive, but not transitive, even after you remove all the fixed points: linear projective space.
Graduate Research Assistant: Michael Merkle
Research Interns:
- Holly Miller
- Violet Nguyen
Faculty Mentor: Harry Bray
Description: The purpose of this project was to use crochet as a medium to display different geometric surfaces with constant curvature and their discrete tilings. Our designs and models are crafted from public knowledge of crocheting techniques and the book Crocheting Adventures with Hyperbolic Planes by Daina Taimina. Team-designed patterns for the Ideal Crochet Sphere and Hyperbolic Flower are linked below. Additionally, this project achieved collaboration with the geometry lab from UVA for an exhibition of our designs at a farmer’s market.

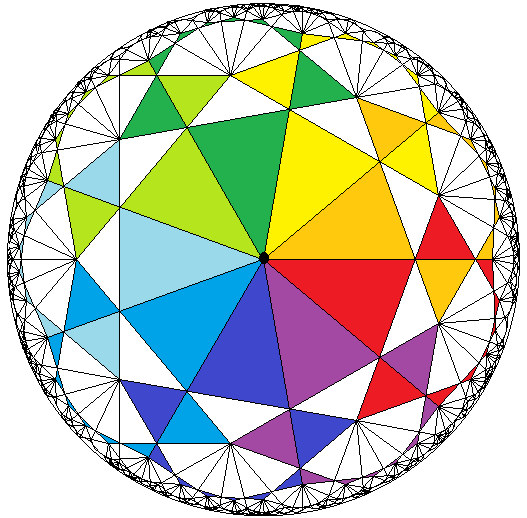

Graduate Research Assistant: Madeline Horton
Research Interns:
- Nhuphuong Au
- Merold Saffa
- Aidan Self
- Sydney Thu
Flower Crochet Pattern: Click Here
Ideal Sphere Crochet Pattern: Click Here
Faculty Mentor: Douglas Eckley
Description:
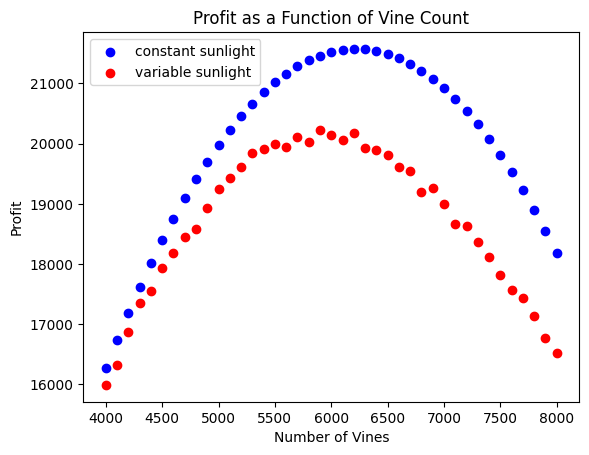
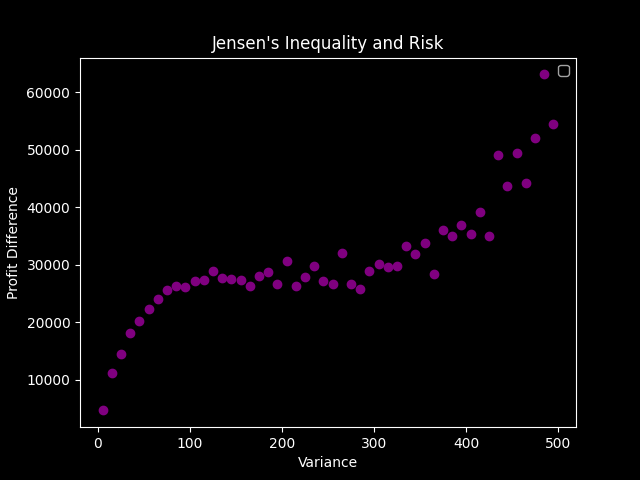
The Polar Method is a type of rejection sampling algorithm that produces two normally-distributed random variables by first simulating two uniform random variables. Similar to the Box-Muller method, the Polar Method relies on the Rayleigh distribution to prove that the magnitude of the simulated values produces two normal random variables. Our goal within this project was to obtain an array of hours of sunlight to accurately predict how much sunlight a vineyard will get, then calculate how many vines we should grow in that vineyard to maximize our profits from producing wine. We compared the deterministic sunlight variables (all constant to 6 hours per day) to the randomly generated simulations of sunlight. The difference between the two predictions can be explained in part by Jensen’s inequality, which limits the mean of the profits to always being smaller than or equal to the profit of the mean outcome. We found that the simulated array causes the maximum expected profit to fall to $20,143, based on 5,990 vines planted, which is lower than the profit measured using the constant variable. Based on those results, we can conclude that we do profit by buying the vineyard and growing the specified amount of vines from the simulated maximum amount of profit, and that the constant value overestimates our profit too much. For future work on this project, we would try to account for other variables that would affect sunlight in our vineyard, including the possibly drastic affects of climate change.
The following two figures show the results of simulating the predictions by using a constant value for the daily amount of sunlight and the values generated from the Polar Method. The difference between the two is analyzed by Jensen’s inequality, which shows the range in which the expected maximum profit should lie.
Research Interns:
- Aleksei Miles
- Jessica Nguyen
- Salina Tecle
- Ethan Walter
Faculty Mentor: Professor Ben Schweinhart and Professor Erika Roldan
Description:
The project, “Random 3D Polyforms”, executed by Dhruv Gramopadhye, James Serrano, and Khoi Tran from George Mason University’s Mathematical and Computational Sciences Laboratory (MEGL), aimed to explore the intriguing world of polyforms. Polyforms are figures constructed by joining identical polytopes connected by at least one of their faces. In this particular project, the researchers focused on a class of polyforms composed of connected cubes, with each cube in the polyform strongly connected by one of its two-dimensional square faces.
The team was particularly interested in understanding the homology of the generated polyforms, such as the number of holes (Betti numbers), and the size of the site perimeter. This semester’s research was centered around how the percolation probability of a given distribution of polyforms impacts its Betti numbers.
The project was based on a work-flow that began with the generation of a connected point cloud with a specified number of points. This was followed by the use of the Metropolis Hasting (MH) Algorithm to shuffle the points a certain number of times. The team then generated a cubical complex from the point cloud, and utilized tools in Persistence Theory to compute the homology of the generated cubical complex. The final step involved studying how the homology changed depending on how the polyforms were generated.
The team encountered challenges and had to overcome bugs, particularly one that caused an incorrect modification of the percolation probability. They also implemented several optimizations, including an early stopping condition that provided a 30-40% speedup, and a heuristic.
Future work includes a full re-write of certain sections to try to eliminate the bug in sampling from the Bernoulli distribution. Additionally, the team aims to generalize the shuffler to support connectedness models such as permutohedra and corner connectedness.
The project was executed under the guidance and mentorship of Shrunal Pothagoni and Dr. Ben Schweinhart. The project findings contribute to the growing body of research on polyforms and their potential applications in computational topology and image processing among others.

Graduate Research Assistant: Shrunal Pothagoni
Research Interns:
- Dhruv Gramopadhye
- James Serrano
- Khoi Tran
Faculty Mentor: Yiannis Loizides
Description: The purpose of this inquiry was to study the classification of foliations on surfaces and what data is necessary for this classification. In particular, the leaf holonomy of a foliation tells us a great deal of information about the foliation. This was one of the primary interests for this project. Specifically, the holonomy allows us to classify foliations based on the behavior of the foliation around its S 1 leaves. This led to the construction of a notion of a moduli space of foliations on the annulus. Research will be continued individually on this, in search of a “nice” notion of the space of foliations on a particular surface.
Graduate Research Assistant: Quincy Frias
Research Interns:
- Deven Linthicum
- Gabe Lumpkin
Faculty Mentors: Evelyn Sander and Dan Anderson
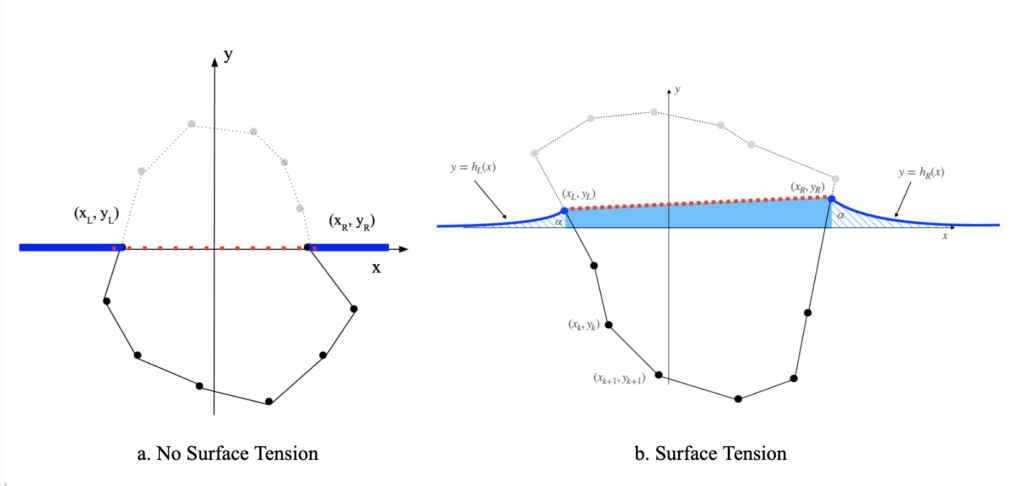
Description: In this undergraduate study, we investigate the behavior of systems of floating 3D-printed objects, specifically pentagonal boats, experiencing surface tension, gravitational, and pressure/buoyant forces. We also considered the imbalance of the horizontal force components acting on the floating boat that occurs during a type of surface motion called Marangoni propulsion. By analyzing the balance of these forces and the Marangoni propulsion phenomenon, we gained a deeper understanding of the statics and dynamics of 3D-printed floating objects and their movement on liquid surfaces.
Graduate Research Assistant: Patrick Bishop
Research Interns:
- Aiden Dunlop
- Phap “James” Nguyen
- Max Werkheiser

Outreach Director: Professor Rosemberg Toala
Description: MEGL offers outreach activities to the community every semester. To fulfill our mission of outreach, we need your help. Participants will deliver, refine and help develop mathematical outreach activities which inspire a passion for mathematics. Check out our website for examples of MEGL outreach activities.
