During Spring 2021 MEGL ran a 5 project program with 24 participants (faculty, graduate, and undergraduate students). The five research/visualization groups are titled:
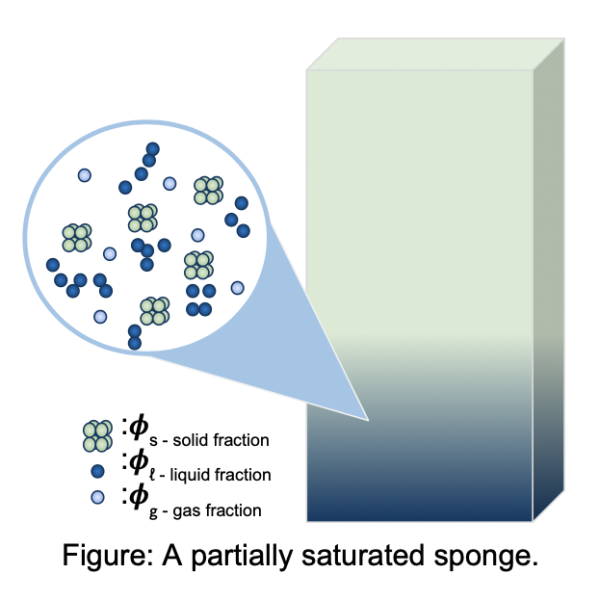
- Mathematical modeling of capillary rise in porous materials
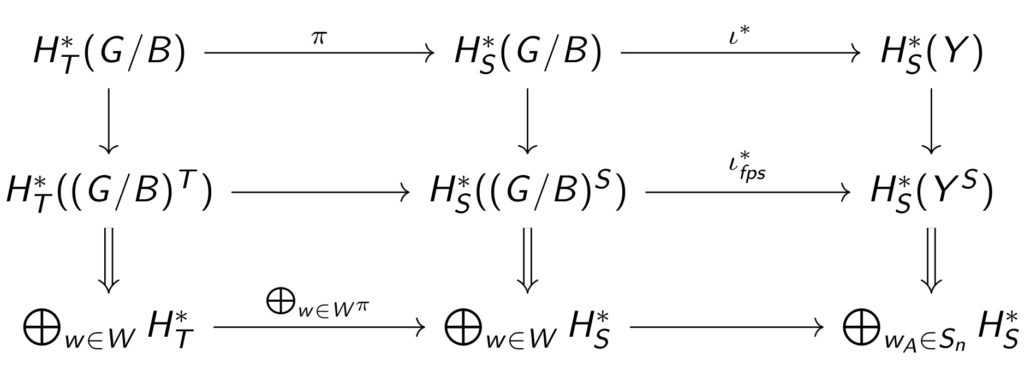
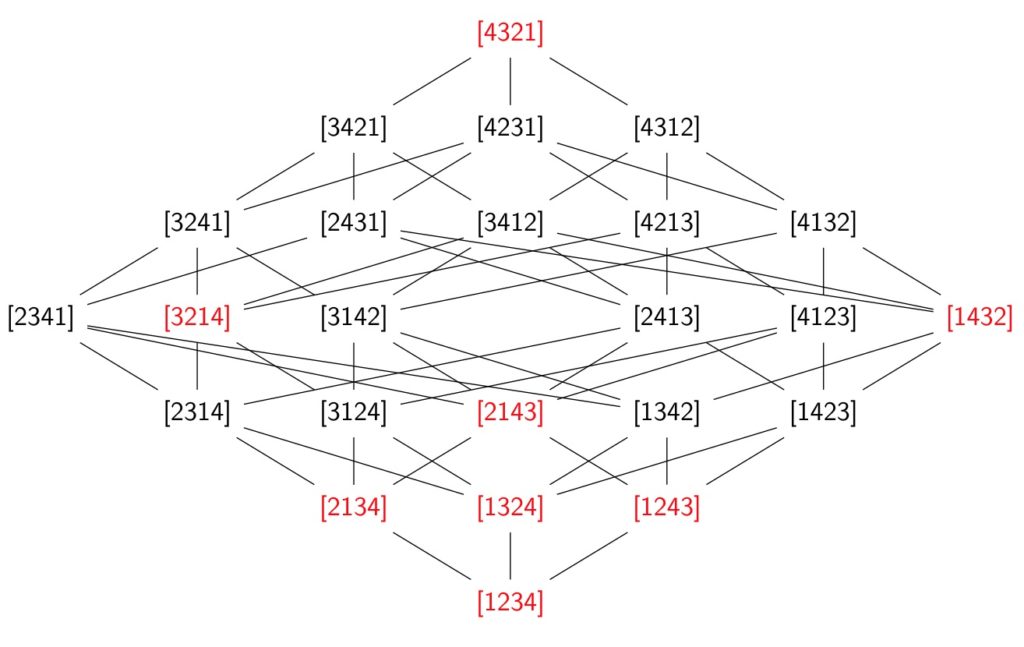
- Combinatorics of Cohomology Rings of Peterson Varieties
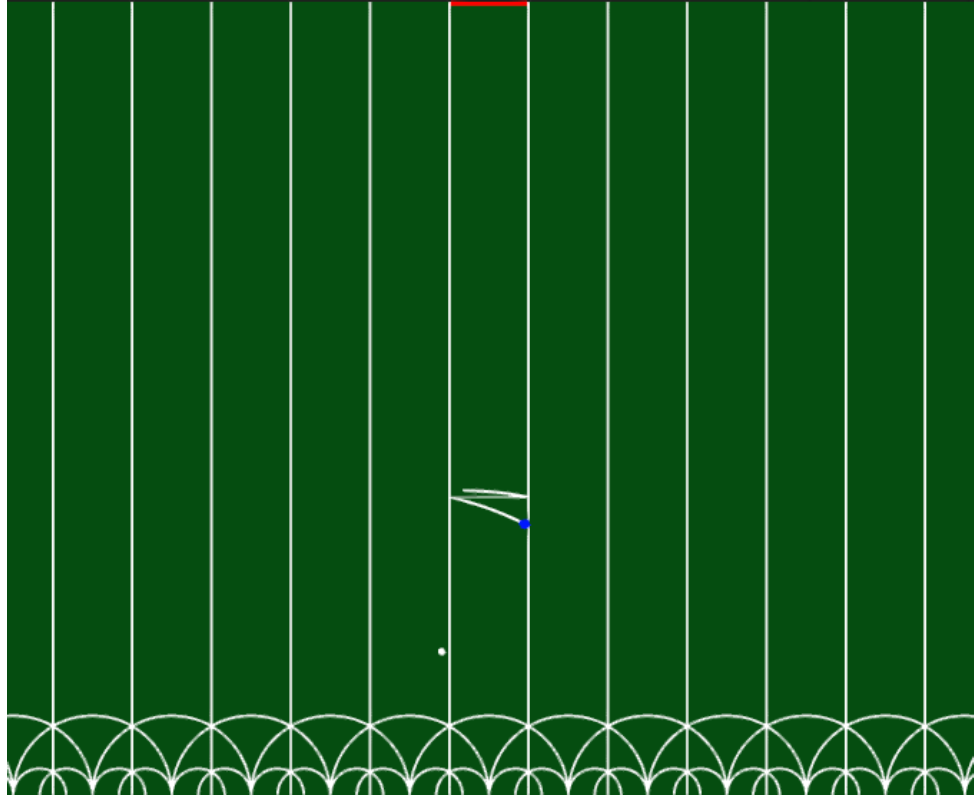
- Mathematical Visualization
- Cores and hulls of ideals of commutative rings
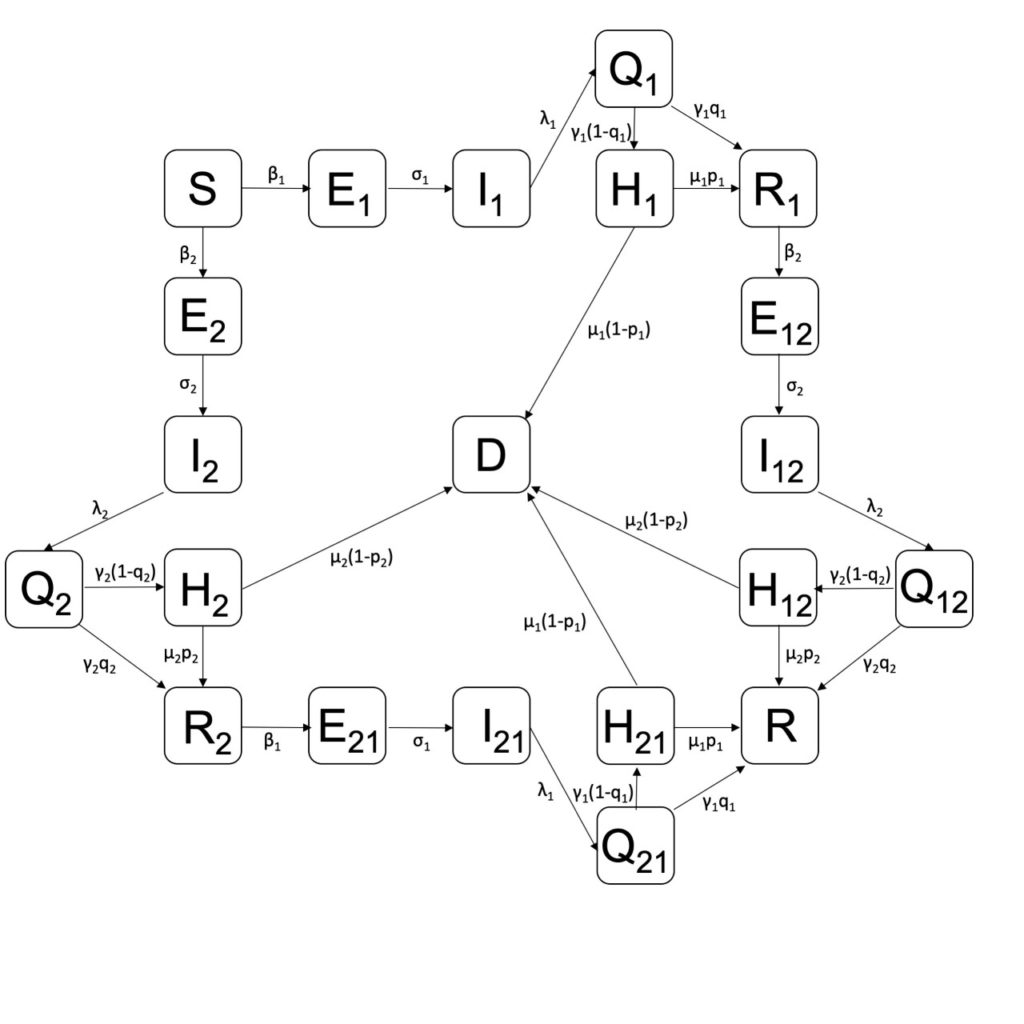
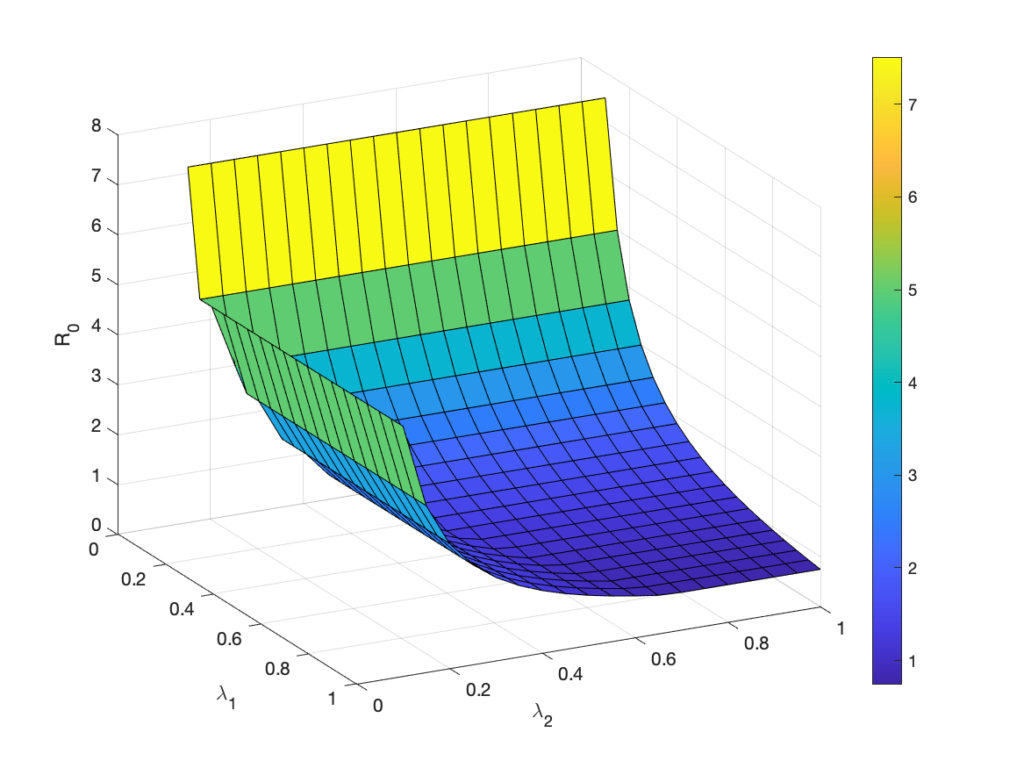
- Mathematical Modeling, Analysis and Control for Understanding the Spread of COVID19
Additionally, there was one public engagement group which we refer to below as Outreach. The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries. We concluded with an end of term symposium and a poster session.
Our end of semester events will be held online.
For full project descriptions go here:
Faculty Advisor: Daniel Anderson
Graduate research assistant: Matthew South
Undergraduate research assistants:
- Laura Nicholson
- Matthew David Kearney
- Zachary Richey
The phenomena of capillary rise of fluid in porous materials is central to many problems in fluid mechanics and has a broad range of applications. Mathematical models describing capillary rise account for the various physical processes involved and are often formulated using differential equations. This project will explore predictive mathematical models and compare results with published capillary rise data as well as with data obtained from simple experiments using familiar porous materials.
Faculty Advisor: Rebecca R.G.
Graduate research assistant: Matthew South
Undergraduate research assistants:
- Aidan Donahue
- Ethan Robert Clelland
- Joseph Bidinger
The task of this project is to compute examples of tight-interiors and *-hulls of ideals in numerical semi-group rings, which are a convenient class of commutative rings. A numerical semi-group ring is a specific type of power-series ring with coefficients in a field. In the context of numerical semigroup rings, the tight-interior operation takes each ideal to a certain maximal subideal. The *-hull operation takes each ideal to a sum of its superideals with the same tight-interior. These operations are new tools which are dual to the notions of tight-closure and *-cores, which themselves are important objects of study in commutative algebra. The motivation in computing new examples of tight-interiors and *-hulls is to build a better sense of their use in characterizing commutative rings and to better our understanding of the tight-closure and *-core operations.
Faculty Advisor: Padhu Seshaiyer
Undergraduate research assistants:
- Samuel Thomas
- Susan Tarabulsi
As COVID-19 cases continue to rise globally, many researchers are continuing to develop mathematical models to help capture the dynamics of the spread of the infection. The compartmental SEIR model and its variations have been widely employed to study COVID-19. These models differ in the type of compartments included, nature of the transmission rates, seasonality, social behavior and several other factors. In this project, we introduced a new multi-variant COVID-19 model that helped provide insight into the dynamics of the spread. Specifically, the dynamics of the sub-populations were modeled through a coupled system of ordinary differential equations. The basic reproduction number for this model is derived that can potentially inform policy makers to make data-driven decisions. We also performed simulations to study the influence of various parameters employed in the model.
Faculty Advisor: Rebecca Goldin
Graduate research assistant: Joseph Frias
Undergraduate research assistants:
- George Andrews
- Swan Klein
- Taylor Fountain
Our goal was to express the restriction of Schubert classes to the Peterson variety as a linear combination of Peterson classes. We used Billey’s Formula to compute restrictions of fixed points of the Flag variety, of which the Peterson variety is a subvariety, which gave us Schubert classes corresponding to each fixed point. We could then compute the pullback of each Schubert class and write this as a linear combination of Peterson classes. We used MatLab and Sage to write code to do these computations, but this quickly becomes computationally expensive. After getting the code to work, we conjectured combinatorial formulas based on patterns observed in the pullbacks. Future work will involve proofs of these conjectures, making additional conjectures after observing new relationships, and improving the efficiency of the code.
Faculty Advisor: Anton Lukyanenko
Graduate research assistant: Joseph Frias and Don Brusaferro
Undergraduate research assistants:
- Ananth Jayadev
- Clarissa Benitez
- Daniel James Heilman
This semester we worked on two previously made games called Snakes on the Plane and
Hyperbolic soccer. We broke up into teams and tackled each project with the overall goal of
improving the educational aspect of the games so the overall topic was clear to the player. This
involved updating code, aesthetics and adding elements to the games so that it held people’s
attention and better displayed the intention of the game.
Originally, Snakes on the Plane was outdated and could use more elements to show a
player what was the connection between the polygons and geometric surfaces. We began but
updated the code so it was playable in order to see what problems could be fixed. Throughout
this process we learned about geometric surfaces and the advantage of using a 2D plane to
represent a geometric surface. We learned about the different types of surfaces and how to apply
Euclidean geometry to them. It was interesting to see how gluing a rectangle in different ways
resulted in a range of surfaces and what characteristics that changed. Overall, we were able to
accomplish a better depiction of these surfaces by adding gifs of the surface rotating and
therefore as someone played the connection between translating across the plane and moving
across the surface was clearer.
The “Hyperbolic Soccer” team made several visual changes to code base in Unity to
make the concept more universal to a general audience. We used Unity to draw in the playfield
and tiling, reorient the camera to show a larger space, and generate a trace of a projectile’s
position in hyperbolic geometry to show that any given line will ultimately reach a certain
height.
Faculty Advisor: Harry Bray
Undergraduate assistants:
- Susan Tarabulsi
- Aidan Donahue
This semester, we reached 1,114 students in a virtual setting. Demand from elementary classrooms was enormous: of the 35 events run, 31 of those events were with elementary students. We ran the activity “your teachers are lying to you” in virtual format for the first time, and developed a new activity on irrational numbers called “irrational thinking.” We also ran the activities “you can count on monsters,” “really big numbers,” and “playground of the infinite.”
