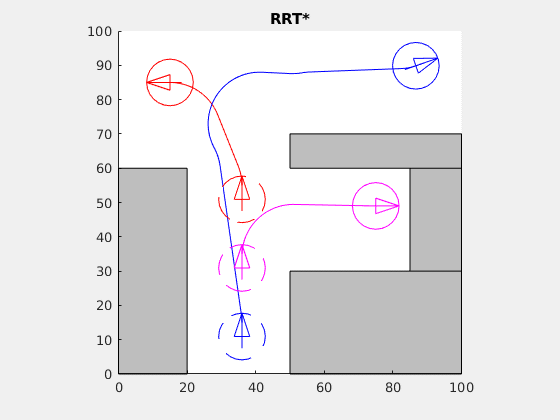
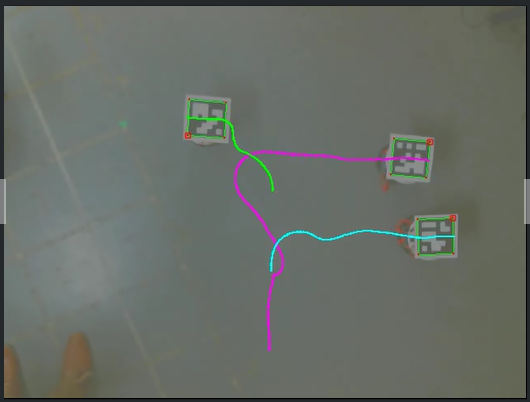
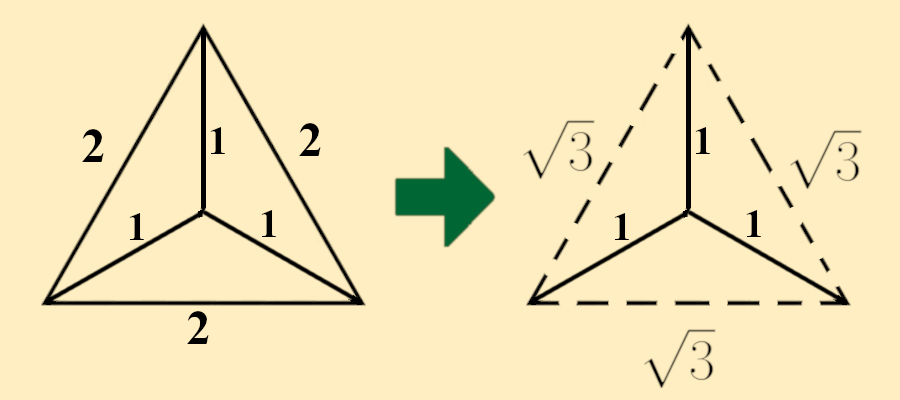
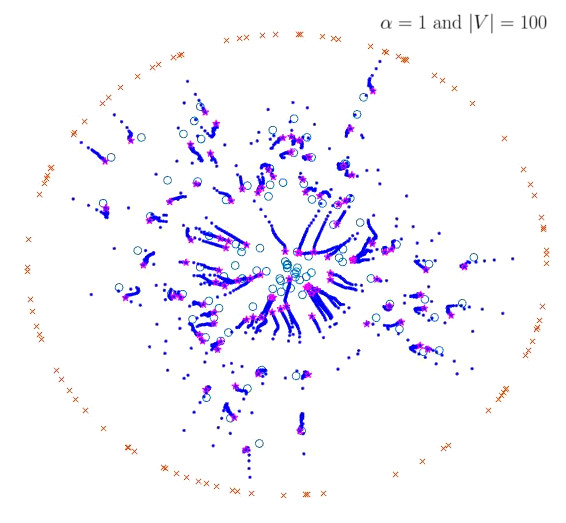
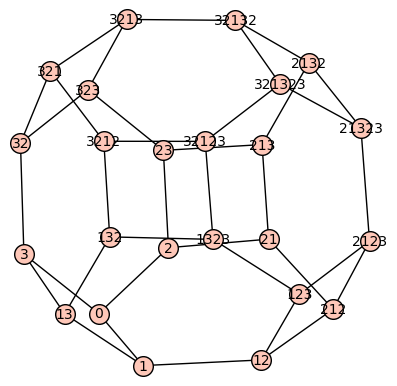
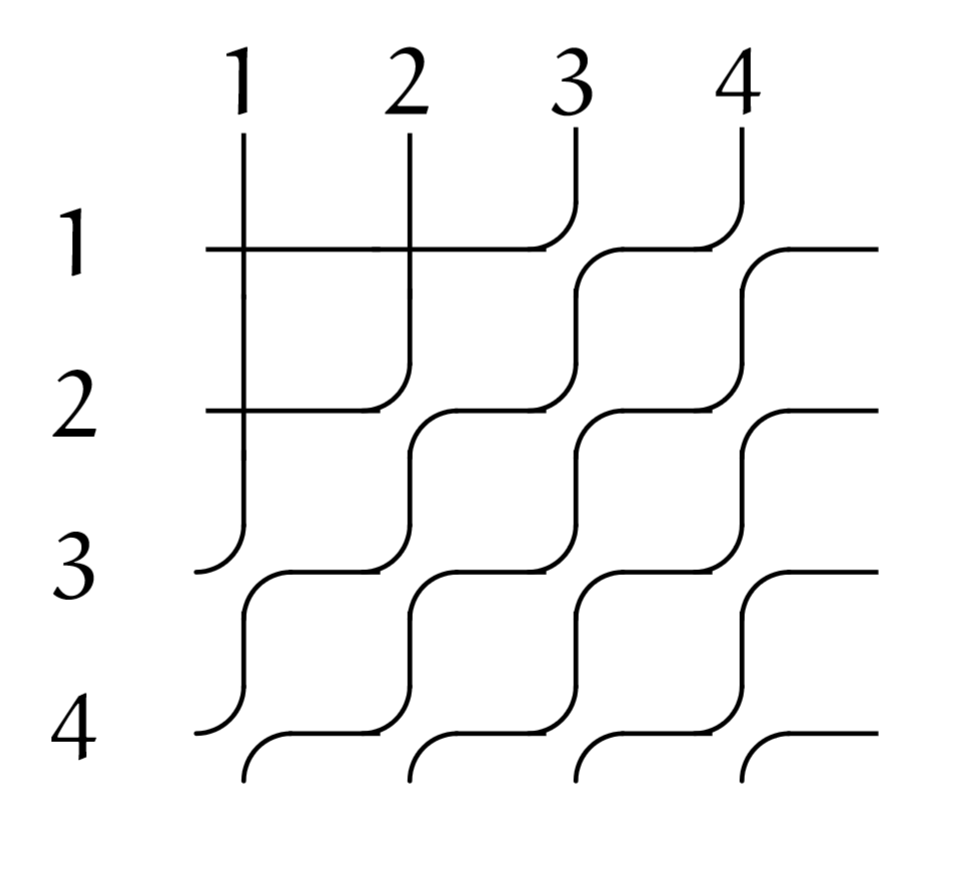
During Spring 2019 MEGL ran a 6 project program with 20 participants (faculty, graduate, and undergraduate students). The five research/visualization groups were titled: Cooperative Parking for Self-Driving Cars, Computations of test ideals of Big Cohen-Macauley modules, Geometry of Complex Networks, Geometric Flows and Dimension Reduction, and Equivariant K-theory of Flag Varieties. Additionally, there was one public engagement group which we refer to below as Outreach. The research/visualization groups engaged in experimental explorations involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and public libraries. We concluded with an end of term symposium and a poster session (scroll down for pictures).
Self-Driving cars are quickly being integrated into society, but there are still lacking any motion-planning algorithms that effectively find paths for multiple cars. In our work, we aim to efficiently produce a motion-path that near-optimally choreographs multiple cars toward a specified location in our space. The purpose of designing this algorithm is to cooperatively park self-driving cars. On top of studying the properties of motion-planning algorithms with multiple cars, we also have developed simulations of the path-finding process and we have used the Mason Autonomous Robotics Lab’s Flock-bots in order to simulate this physically. On the algorithmic side, our team worked on extending the motion-planning algorithm RRT, Rapidly-Exploring Random Trees Star, to work with multiple cars while also retaining the algorithm’s inherent convergence properties as well as developing a multi-car real-time algorithm. On the robotics side of the project, our team worked on taking the paths generated by the computational simulations of the multiple car RRT and using those to guide Flock-bot motion, effectively emulating self-driving cars.
This project was focused on computing the test ideals of finitely generated Cohen-Macaulay modules of various rings. Given a module, $M$, over a complete local domain, $R$, the test ideal, $\tau_M(R)$, is the (internal) sum of the images of $R$-linear maps from $M$ to $R$. The rings we study primarily include subrings and quotients of polynomial rings and power series rings.
If $R$ is a nonsingular complete local domain, then for any finitely generated Cohen-Macaulay module, $M$, we have $\tau_M(R)=R$. Thus, computing the test ideals of the finitely generated Cohen-Macaulay modules can give an idea of how close a complete local domain is to being nonsingular: vaguely, the larger the test ideal, the less singular the ring, and vice versa.
A complex network is a graph, $G = (V, E)$ consisting of $E$ edges and $V$ vertices with non-trivial features, such as sparseness, algebraic degree distribution, community structure, and exponential growth of neighbors, that often occur in graphs modeling real world systems. We aimed to study the geometry of complex networks by developing an embedding, or mapping, to a metric space that preserves its topological properties. We considered two types of embeddings: isometric and ‘similarity’. An isometric embedding exactly preserves distance in the embedding so the distance between two nodes is equivalent to the distance between their corresponding points in the embedding. In a similarity embedding, we loosen the constraints of the isometric case and we say that if two points are connected in the graph, then their distance is less than or equal to a parameter, $\alpha$, and if they are not connected in the graph, their distance is greater than $\alpha$.
i.e.
$
d_\Omega (f(v_i), f(v_j)) \leq \alpha \quad \mathrm{if} \ A_{ij}=1
$
$d_\Omega (f(v_i), f(v_j)) > \alpha \quad \mathrm{if} \ A_{ij} = 0$
Our research last semester showed that complex networks behave like trees, so we tried to embed our graph into hyperbolic space. To do this, we constructed a cost function that has a cost when disconnected nodes are too close in the embedding and when connected nodes are too far apart.
$
J_i=\sum_{j=1}^n A_{ij} \Phi(d_H(x_i,x_j)^2)+\sum_{j=1}^n B_{ij} \Psi (d_H(x_i,x_j)^2)
$
Then we use the gradient descent algorithm to find a low cost embedding. At first we randomly placed initial points in the hyperbolic plane, but the algorithm would not always converge. In this case, disconnected nodes would meet and become frustrated by a local minimum. To avoid this, we remembered the angular component associated with each point and placed it on the boundary of a disk centered at the origin. This guaranteed good initial conditions and prevented the algorithm from finding local minima.
Given a Riemannian manifold $(M, g)$ with a specified metric $g$ the goal of minimal embedding is to find a smooth map $F : M \to \mathbb{R}^m$ such that: $F(M)$ is isometric to $M$ and has minimal extrinsic curvature. Given a data set, we want to find an algorithm that produces a best-fit of a smooth manifold to that set such that it is minimally embedded. Using Richardson extrapolation and minimization of gradient descent we had success with various example data sets in low dimension.
This semester the group focused on the combinatorial aspects of the equivariant K-theory $K_T(\textrm{GL}_n(\mathbb{C})/B)$ of flag manifolds. Using objects called pipe dreams we can refine the Schubert polynomials previously used as a basis for $K_T(\textrm{GL}_n(\mathbb{C})/B)$ to a basis represented by monomials corresponding to flush left pipe dreams, establishing an explicit decomposition of any formal difference of equivariant vector bundles into a sum of line bundles with coefficients in the representation ring of the n-torus.
In addition, we introduced double Schubert polynomials to represent the K-theory classes of Schubert varieties inside of our flag variety. Our next step is to understand and give combinatorial rules for the decomposition of these Schubert classes into our line bundles.
Our outreach program met its goal of running 15 activities this Spring, reaching over 450 students, including a visit to the Department of Homeland Security’s Kids Day as part of the Nifty Fifty Program. We were also excited to add a new elementary school to our network, Union Mill Elementary, which we visited 3 times over the course of one week, sharing our activity You Can Count on Monsters with the whole of their 3rd grade class.
