-
During Spring 2020 MEGL is running a 6 project program with 21 participants (faculty, graduate, and undergraduate students). The six research/visualization groups are titled:
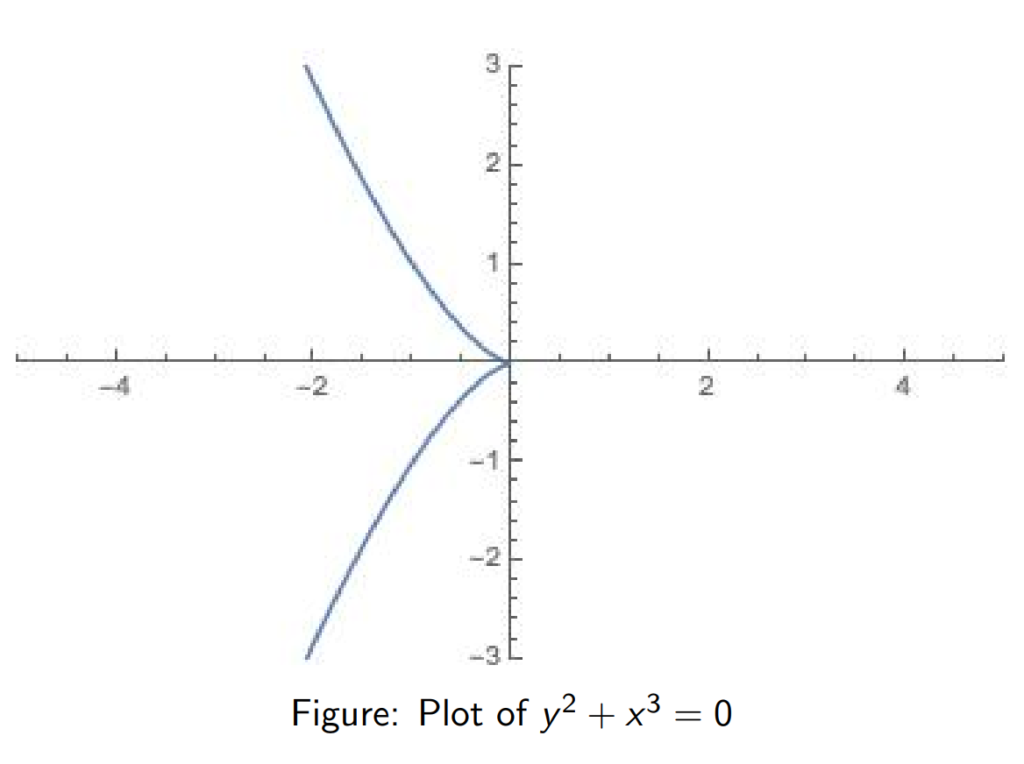
- A computation of test ideals of Big Cohen-Macaulay modules,
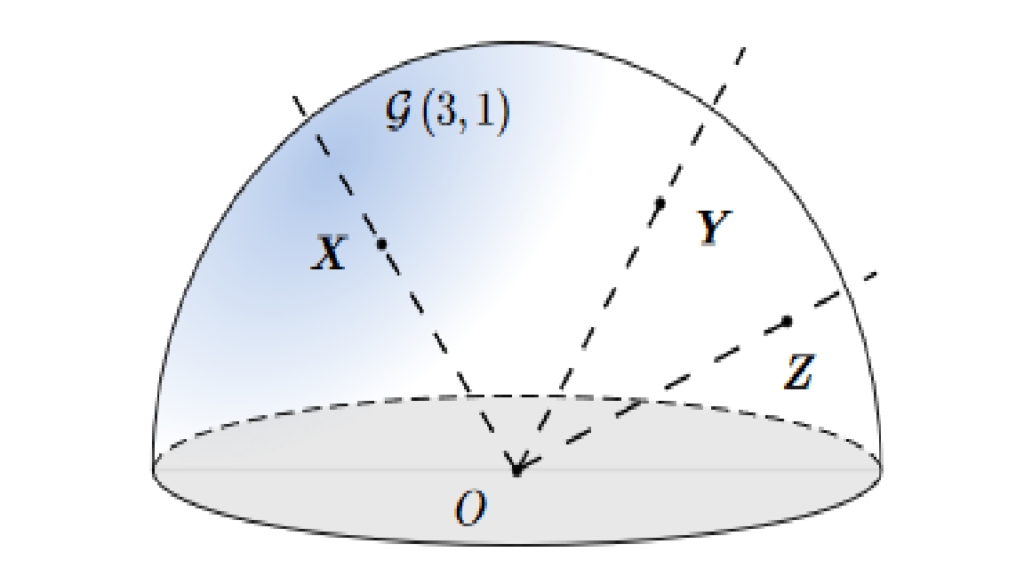
- Thurston Geometries in Virtual Reality,
- Content Formulas in algebras derived from Grassmanians,
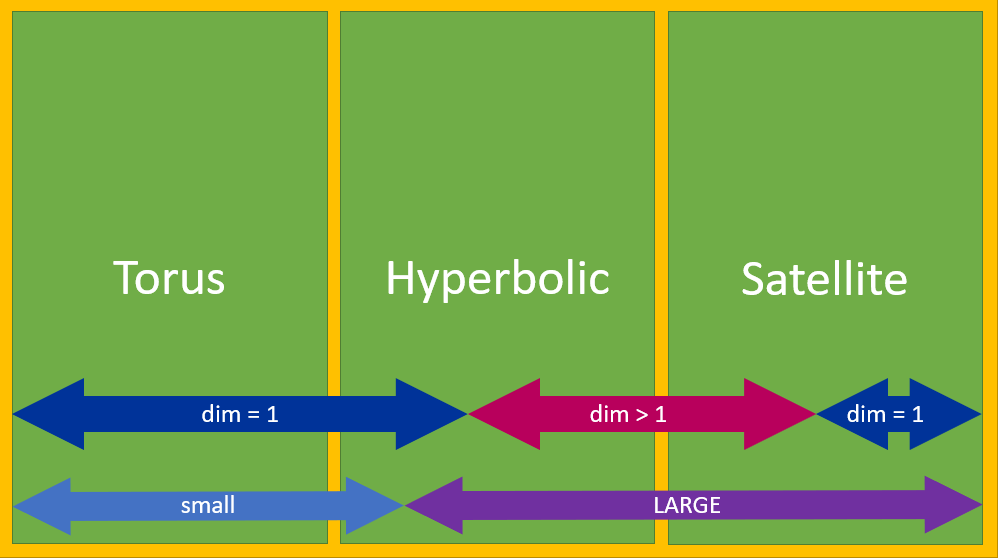
- Statistics in Deformations of Large Knots,
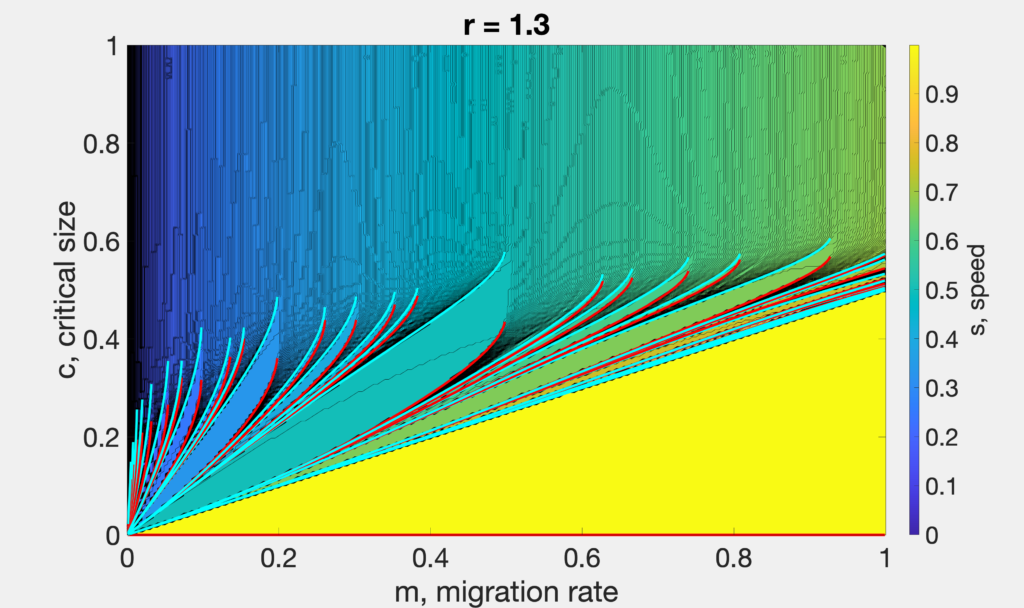
- Instability spreading in spatially extended systems and
- Mathematics Community Outreach.
MEGL Events
All the MEGL events during the second half of the semester were either cancelled or moved online due to Covid-19.
- MEGL Start of the Semester Meeting – 10 am, January 24, 2020
- Mid-semester Meeting – 11 am, March 26, 2020. We will be having a virtual meeting using zoom. Please check your emails for more details.
- MEGL Poster session – Friday, May 8, 2020 (Cancelled due to Covid-19).
- MEGL Symposium(Virtual) – 2:30 – 5:30 pm, May 8, 2020
Faculty mentor: Prof. Rebecca R.G.
Student members:
- Julian Benali
- Shrunal Pothagoni
In our research, we compute the test ideals of finitely-generated CM (MCM) modules of various rings. The rings we study include sub-rings and quotients of polynomial rings and power series rings. The test ideals of such rings yield information about the rings’ singularities and geometric properties: vaguely, the larger the test ideal, the less singular the ring, and vice versa. If the ring is non-singular, the test ideal coming from any MCM module is the whole ring.
Faculty mentor: Prof. Anton Lukyanenko
Student members:
- Jean-Marc Daviau-Williams
- Phuc Truong
- Jeanie Schreiber
Our goal was to create an archery simulation to visualize different Thurston geometries, similar to the work done by Hypernom. To do this, we utilized a free game engine called Unity, as it already had the framework for visualizing things in three-dimensional space. In our simulation, the path of an arrow fired follows the geodesics (straight lines). However, since different geometries have different geodesics, we need to consider these when programming the movement of objects. This semester, we focused primarily on the Nil geometry, which required determining the correct group law on 3-D vectors and ensuring arrow path consistency in the 3-D space. In the end, we found correct equations to use that gave us the desired properties in Unity for the arrows path.
Downloads:
Faculty mentor: Prof. Neil Epstein
Student members:
- Aleyah Dawkins
- Jae-Moon Hwang
- Shrunal Pothagoni
Classically, the content c(f) of a polynomial f in R[X] with leading coefficients in a commutative ring R is the ideal in R generated by the coefficients of f. Gauss’s formula c(f)c(g)=c(fg) generally fails, but Dedekin and Merten (1893) showed that there is always a number n such that c(f)nc(g)=c(f)n−1c(fg). If one replaces a polynomial extension with a Grassmannian extension, one can create a similar content function from R[Grass] to ideals of R and ask the question whether a Dedekind-Mertens formula exists in this content. The goal of research is to attempt to resolve this question to increase our understanding of the algebra of Grassmanians.
Downloads:
Faculty mentor: Prof. Sean Lawton
Student members:
- George Andrews
- Mathew Hasty
- Savannah Crawford
- Matthew David Kearney
The goal of this project was to continue the work of the previous semester; to discover trends in knots based on a measure of “complexity”, the Krull dimension of the knot group’s character variety. By diversifying the types of knots we observed and looking at different classes of knots, we are able to find ways unique to these classes that aided in calculation of the dimensions. Our work this semester has lead to many dimensions being calculated for specific types of knots. This, in turn, has lead to a number of conjectures which suggest a correlation between the dimensions and the knots groups and character varieties of certain types of knots. Future work in this area would include furthering these conjectures and finding more effective ways of computing the Krull dimensions.
Project Page: http://meglab.wikidot.com/lawton1920
Downloads:
Faculty mentor: Prof. Matt Holzer
Student members:
- Wyatt Rush
- Zachary Richey
- Samuel Schmidgall
This research studies waves structures that emerge when a small amount of population is dropped in a one-dimensional, discrete-space, discrete-time, population model. We study the speeds of these waves, and the three types of waves that arise: pushed, pulled, and locked. This project analytically describes all locked waves in this model and compares the results to numerical simulations. We also discuss how locked waves relate to the other types of waves.
Downloads:
Faculty mentor: Prof. Jack Love
Student members:
- Aidan Donahue
- Susan Tarabulsi
This semester was the first semester where MEGL Outreach had an actual team involved. In total, we reached 528 students in Spring 2020, with more to follow in May. We did a number of activities in person, and developed three online variations of existing activities in response to the recent necessity for online learning materials, which we hope to continue offering in the future. In addition to our online talks, we also developed a brand new booth activity showcasing our current activities, which we plan to take to various events around the DMV.
Downloads: