During Summer 2016 MEGL ran a program with 18 participants. There were three research groups (Orbits, Special Words, and Polytopes), two visualization groups (3D Geometric Surfaces and Virtual Reality), and one public outreach group (Outreach). The research and visualization groups engaged in experimental exploration involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, graduate students, and undergraduates to develop and implement activities for elementary and high school students that were presented at local schools and summer camps. We began with a opening BBQ, and concluded with final reports from all teams.

We are studying the dynamics of the action of outer automorphism group, $Out(F_2)$ on the character variety, $\mathfrak{X}(F_2,\mathrm{SL}_2(\mathbb{F}_q))$ for a prime $q$. One of the ways to understand the dynamics is looking at the growth of the maximum orbit length with the increase in prime $q$. We analysed the orbit growth of few outer automorphisms using Mathematica. The elements of $Out(F_2)$ exhibiting a logarithmic growth rate in the maximum orbit length is particularly interesting. Using Mathematica enabled the visualization of orbits in $\mathbb{F}_q^3$. We were also able to identify some elements of $Out(F_2)$ whose maximum orbit length is the same.
A possible future course is to determine the arithmetic ergodicity of the above action, in particular, the action of the subgroups generated by a subset of generators of $Out(F_2)$.
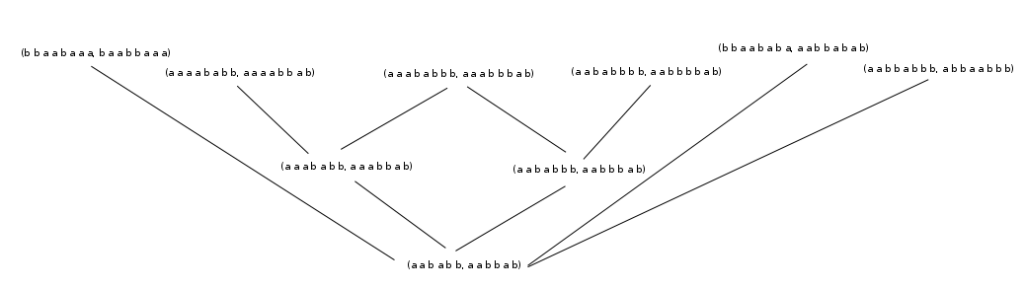
Special words are sets of non-conjugate words that are trace equivalent. The words we use are elements of the rank 2 free group. The trace of a word is calculated by replacing each letter with a corresponding matrix from $SL_2\mathbb{C}$.
Two words are considered trace equivalent if they have the same trace for all choices of $SL_2\mathbb{C}$ matrices. Words are considered 2-special if $SL_2\mathbb{C}$ matrices are used, 3-special if $SL_3\mathbb{C}$ matrices are used, and so on. This research is to determine necessary conditions for words to be 3-special with the goal of determining if 3-special words exist at all. It has been previously proven that a word will never be 3-special with its inverse. We conjecture that a word will never be 3-special with its reverse and alpha automorphism image, the mapping which takes each letter to its inverse. We have proven this for most cases of the alpha automorphism and are working on proving it for the rest of the alpha automorphism cases and all reverse cases using the $SL_3$ Fricke polynomial. We have developed a computer program that calculates a unique $SL_3$ Fricke polynomial for any word to assist in proving these conjectures. This research has applications to algebraic geometry.
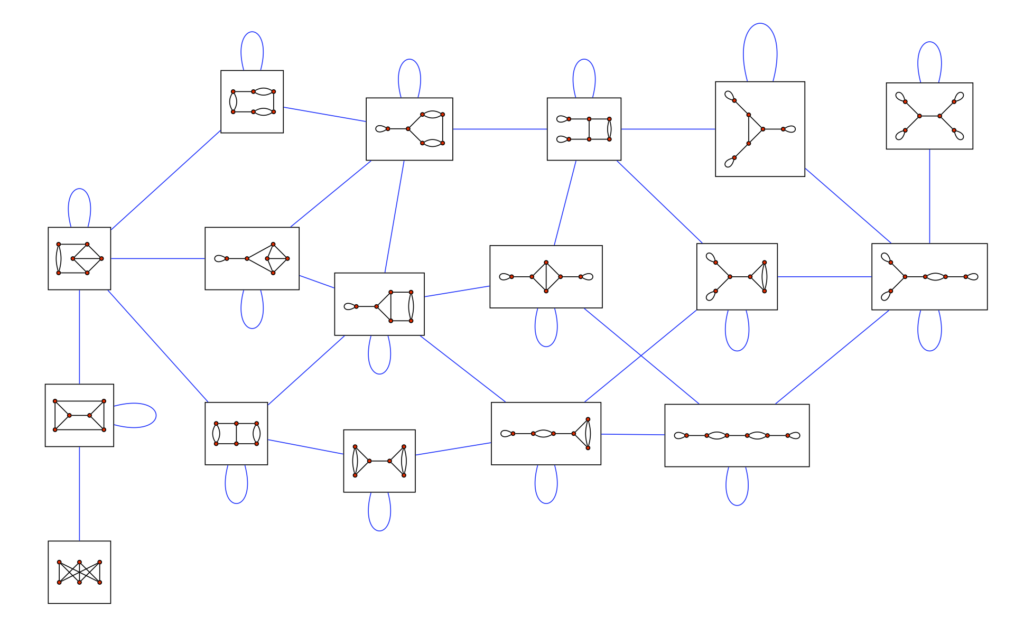
The purpose of this summer’s project was to enumerate the Hilbert and Markov bases for polyhedral cones that come out of gluing Berenstein-Zelevinsky ([http://arxiv.org/pdf/1308.4888v1.pdf BZ]) triangles according to trivalent multigraphs. The Hilbert basis is the minimal set of integer vectors that span the polyhedral cone, while the Markov basis is the minimal set of relations in the semigroup generated by the Hilbert basis. Using the Hilbert and Markov bases, we can present the semigroup algebra of the cone lattice. Using Python code, we could translate a graph and type of BZ triangle into a set of relations among the coordinates of the cone. We could then input this into [http://www.4ti2.de/ 4ti2] to get our Hilbert and Markov bases. We compiled a spreadsheet of such bases, defined by the graph and type of triangle.

This summer, we had the opportunity to improve on our previous demonstration of Drs. Ramras (IUPUI) and Pengelley’s (NMSU) paper on the nullhomotopy of the double twist in $SO(3)$. We added some features, such as the ability to turn on and off each of the (now) multiple curves in the frame view, and added a credits scroll. Our demo will be featured in the acknowledgments section of Ramras’ and Pengelley’s paper, which will be published in the the journal //The Mathematical Intelligencer//.
Turning to the future, we are working on visualizing hyperbolic spaces using virtual reality. Work is being done on porting [http://geometrygames.org/CurvedSpaces/ Curved Spaces] to Unity or Unreal Engine. This game can render visualizations of hyperbolic 3-manifolds using sets of isometries of hyperbolic space.
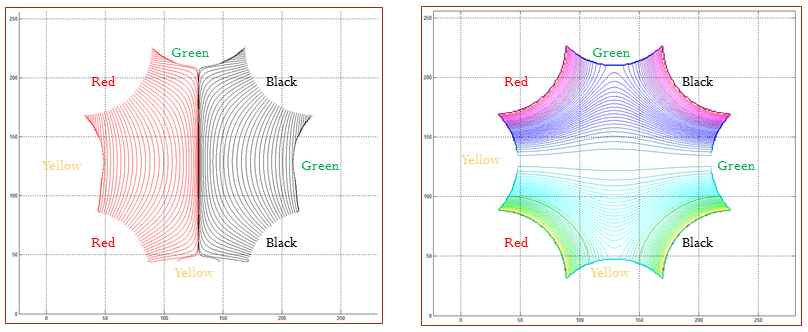
In the 1950’s, Nash and Kuiper proved existence of $C^1$ isometric embed-dings (or immersions) of Riemannian manifolds into higher dimensional Euclidean space. Two decades later, Gromov invented the convex integration technique, providing the tool for the construction of $C^1$ isometric embeddings. From 2006 to 2012, three French mathematics institutions collaborated in the Hevea Project to produce a 3D model of an isometric embedding of a at torus in 3D Euclidean space. In previous work, we formulated an alternative and simplified approach to constructing such an isometric embedding that is more easily extendable to other surfaces. One of our follow-on goals is to develop a construction of an isometric embedding of a hyperbolic octagon to a double torus. Before this isometric embedding could be achieved, it is first necessary to establish an embedding. Furthermore, the embedding must be conformal because all isometric maps are conformal. In this paper, we attempt to construct a conformal embedding from a hyperbolic octagon to a double torus; however, there are still flaws in this construction.

During Summer 2016 MEGL Outreach held two outreach activities, developed a new activity, and secured a fall calendar that exceeds the previous semester’s.
The outreach activities were Really BIG Numbers, held at Hunters Woods Elementary School for their Young Scholars program on July 27, and Snowflakes and Symmetry, a new activity developed over the summer, held at George Mason University on July 14 for the F.O.C.U.S. (Females Of Color Underrepresented in Stem) summer program.
Our network in the K-12 educational community continues to grow. As of July 29 we have 15 scheduled activities for the Fall semester, already surpassing our 12 activities from the Spring, and are well on track to reach our goal of 20 activities for the Fall and get a head start on filling our Spring 2017 calendar.


