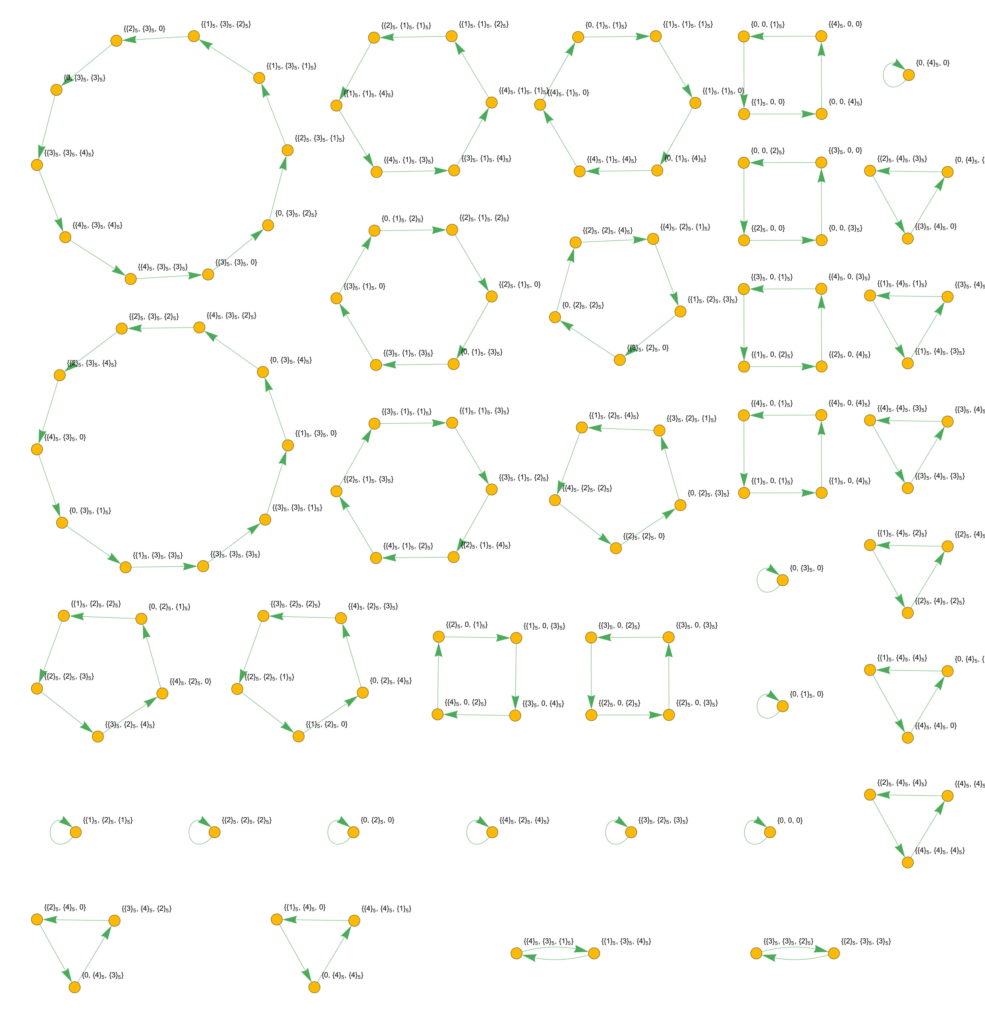
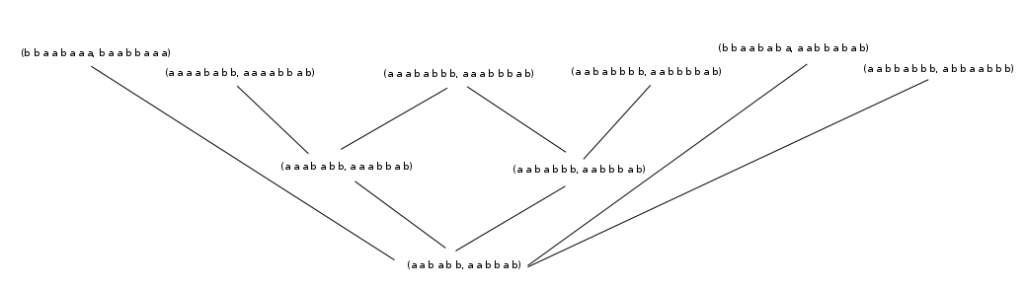
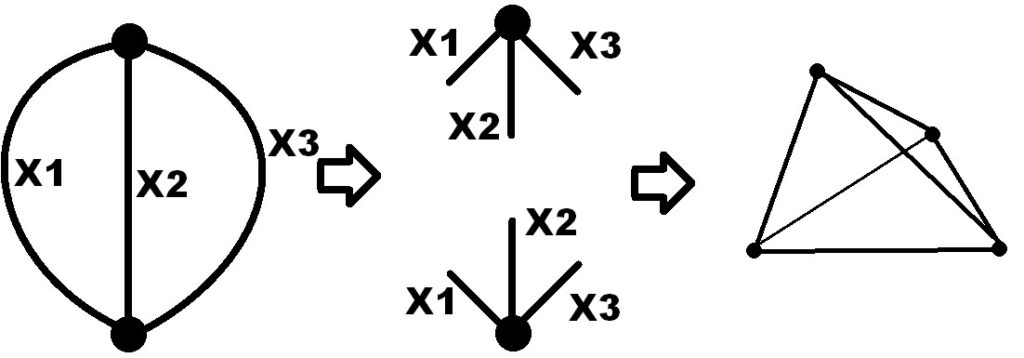
During Summer 2015 MEGL ran a 20-participant program (its inaugural program). There were three research groups, named: Orbits, Special Words, and Polytopes. Each of these group engaged in experimental research involving faculty, graduate students, and undergraduates.
Teams met weekly to conduct experiments generating data, make conjectures from data, and work on theory resulting from conjectures. Additionally, there were development teams in Virtual Reality, 3D Printing, and Community Engagement. The summer ended with a Symposium where all teams presented their work, and with a significant participation in the 2015 Geometry Labs United Conference (where all three research teams placed in the research poster competition; including first prize).
This team included undergraduates Robert Argus, Patrick Brown, and Jermain McDermott, visiting graduate student Diaaeldin Taha, and faculty adviser Dr. Sean Lawton.
The project was to explore the nature of the periods resulting from certain dynamical systems. In particular, let $\mathfrak{X}= \mathrm{Hom}(F_r, \mathrm{SL}(2,\mathbb{F}_q))/\!\!/ \mathrm{SL}(2,\mathbb{F}_q)$ be the $\mathbb{F}_q$-points of the [*https://en.wikipedia.org/wiki/Character_variety character variety], where $ F_r $ is the [[[https://en.wikipedia.org/wiki/Free_group| free group]]] of r letters, and $ \mathbb{F}_q $ is the [[[https://en.wikipedia.org/wiki/Finite_field| finite field]]] of order q. Then $\mathrm{Out}(F_r)$ acts on $\mathfrak{X}$ by $\chi\mapsto \chi\circ \alpha$ for a given $\alpha\in \mathrm{Out}(F_r)$. Upon fixing $\alpha$ and considering the resulting dynamical system for a fixed $\chi$, we were interested in the length of the orbits and how it changes as a function of $q$.
This team included high school student Vishal Mummareddy, undergraduates Patrick Bishop , Mary Leskovec, and Tim Reid, visiting graduate student Clément Guérin, and faculty adviser Dr. Sean Lawton.
The project was to classify and search for special words in free groups. Special words are pairs of elements of a rank $r$ [[[https://en.wikipedia.org/wiki/Free_group| free group]]] $F_r$ which are not cyclically equivalent but have the same trace function. The trace function for a fixed word $w\in F_r$ is defined by sending an $r$-tuple of determinant one matrices to a number obtained by replacing each letter of $w$ with the corresponding entries of the $r$-tuple of matrices, multiplying the matrices according to the structure of $w$, and adding the values on the diagonal of the resulting matrix.
This team included undergraduates Austin Alderete, Conor Nelson, James Chiriaco Ⅱ, and Mezel Smith, visiting graduate student Cigole Thomas, and faculty mentor Dr. Christopher Manon.
The team worked on studying the combinatorics of the phylogenetic semigroups of trivalent graphs and the polytopes that arise from them. This initial work provided a means of identifying the generators of the semigroup corresponding to the extremal rays of the related polytope by specific paths on the graph.
