During Fall 2015 MEGL ran a 15-participant program. There were six research groups, named: Orbits, Special Words, Polytopes, Outreach, 3D printing and Virtual reality. Each of these group engaged in experimental research involving faculty, graduate students, and undergraduates. Teams met weekly to conduct experiments generating data, make conjectures from data, and work on theory resulting from conjectures. The fall semester ended with a Symposium where all teams presented their work.
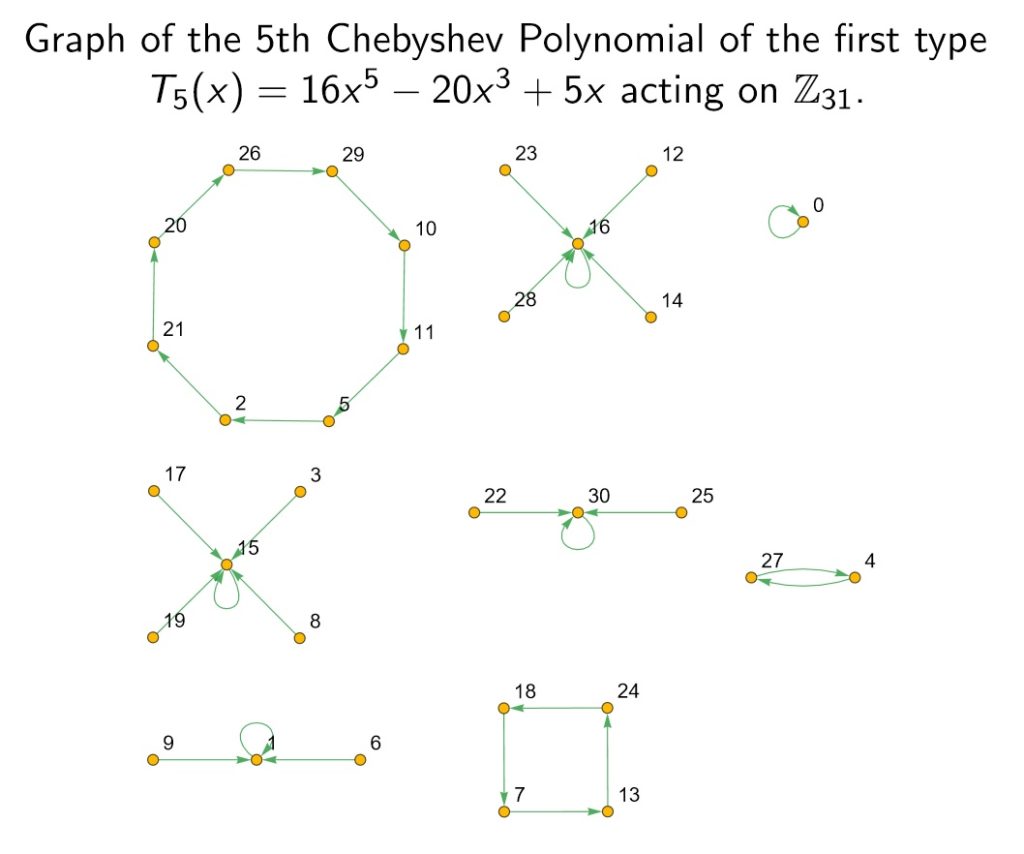
Let $F_r$ denote the free group on $r$ symbols, $\mathrm{SL}(n,\mathbb{F}_q)$ is the special linear group of $n\times n$ matrices over the finite field of order $q$, and $\mathrm{Hom}(F_r, \mathrm{SL}(n,\mathbb{F}_q))$ the set of group homomorphisms from $F_r$ to $\mathrm{SL}(n,\mathbb{F}_q)$.We have been studying a particular discrete dynamical system where the state space is the character variety obtained from a geometric invariant theory quotient $\mathrm{Hom}(F_r, \mathrm{SL}(n,\mathbb{F}_q))//\mathrm{SL}(n,\mathbb{F}_q)$ (we shall denote this by $\mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))$). The elements of $\mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))$ are equivalence classes of homomorphisms; we will denote $[\rho]$ for the equivalence class of $\rho \in \mathrm{Hom}(F_r, \mathrm{SL}(n,\mathbb{F}_q))$. The discrete dynamical system of interest is based on the right-group action of $\mathrm{Out}(F_r)=\mathrm{Aut}(F_r)/\mathrm{Inn}(F_r)$ (which we call the outer automorphism group) on $\mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))$, where $[\rho]\cdot [\alpha]=[\rho(\alpha)]$. For a fixed outer automorphism $[\alpha]$, the dynamical system has the rule of evolution $R_{[\alpha]}:\mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))\times \mathbb{Z}\rightarrow \mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))$ where $R_{[\alpha]}([\rho],n)=[\rho(\alpha^n)]$. Our aim is to better understand the forward orbits, i.e. the sequences $[\rho],[\rho(\alpha)],[\rho(\alpha^2)],…$ for a fixed $[\alpha]$. We started with the case of $\mathrm{SL}(2,\mathbb{F}_q))$ looking first at $F_1$ (where we studied “outer injections” or $\mathrm{Inj}(F_1)/\mathrm{Inn}(F_1)$ instead of $\mathrm{Out}(F_1)$) and are currently studying the orbits for $r=2$. The main question we have been asking is:
For a fixed $[\alpha]\in \mathrm{Out}(F_2)$, can we find a function in the order of the finite field $F(q)$ that gives the largest prime period over all elements of $\mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))$? (The maximum positive integer $n$ such that there exists $[\rho]\in \mathfrak{X}_r(\mathrm{SL}(n,\mathbb{F}_q))$ with prime period $n$ under $[\alpha]$)
Over the course of previous semester, Special group has made some results in the categorization and pursuit of special words. Some of which is we proved that the automorphism image of any pair of special words will also be special. We used the idea of an “anti-automorphism”, a relation having all the properties of an automorphism, but reverses order, instead of preserving order. Thus if $\phi$ were an automorphism, $\phi(abc) = \phi(c)\phi(b)\phi(a)$. We proved as well that the anti-autorphism image is also special. In searching for SL3 special words, we made a significant amount of elimination by proving all words and their inverse are not 3 special. We define signature of a word as the ordered tuple of un-ordered exponents, where the exponents of a go first and then the exponents of b. For example, the signature of $a^2b^2ab^{-1}$ is $\{ {2, 1}, {2, -1}\}$. We have proven that the signatures of SL3 special words must be the same. From this we know that in most cases, a word will not be special with its reverse inverse image, we have used this to prove that in the same cases, a word will not be special with its reverse image. The case where these proofs do not apply is where the word and its inverse reverse image have the same signature. An example of this is the word $ab^{-1}a^{-1}b$ whose inverse reverse image is $b^{-1}aba^{-1}$. Both words have the signature $\{ {1,-1},{1,-1}\}$.
The Locus we are currently exploring requires a word to have the same signature when the alpha automorphism is applied to it. This means the word and its inverse reverse have the same signature. Currently the program we are writing is meant to generate a data set of these words and then to test them for 3-speciality.
This team included undergraduates Austin Alderete, Conor Nelson, and Mark Tuben, graduate student Shams Alyusof, and faculty mentor Dr. Christopher Manon.
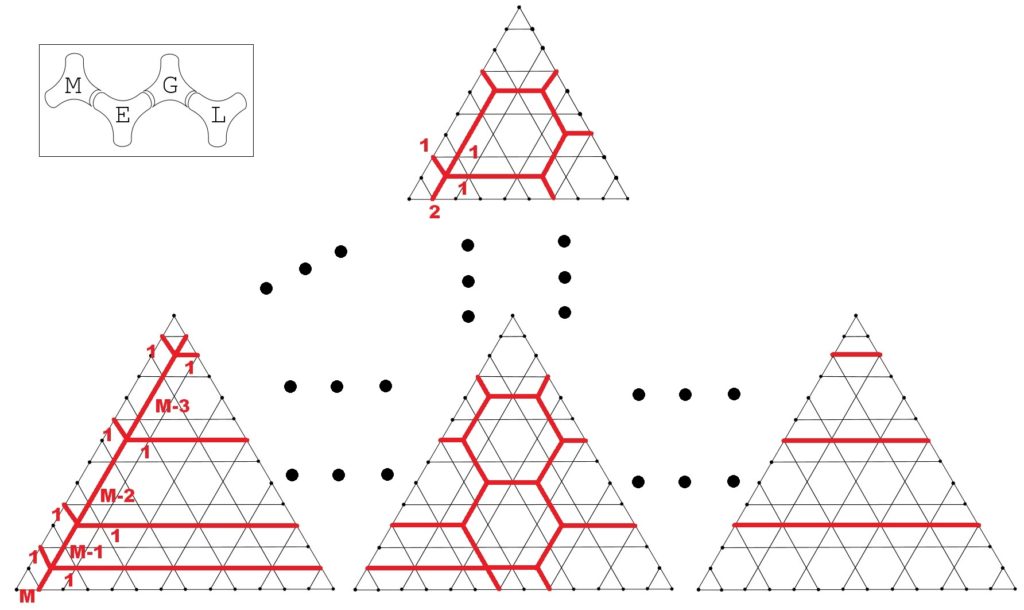
Previous work focused on the study of the phylogenetic semigroup of trivalent graphs and their associated polytopes. The summer team’s work classified the generators corresponding to extremal rays in the polyhedral cone.
Building on this, the fall team studied a generalization of the semigroup formed by considering arbitrary but fixed sized Berenstein-Zelevinsky triangle quilts of trivalent graphs, also known as $BZ(SL_m(\mathbb{C}))$. It was shown that for either a fixed $m>2$ or a fixed graph (but not both), no bound existed for the maximum weight of generators present across all such semigroups.
This result shows the vast increase in difficulty associated with classifying the generators of these semigroups. Future work is likely to attempt to find a minimal generating set or to classify only those generators associated to extremal rays.

Virtual reality technology is an exciting, growing tool not only in the entertainment realm, but in the educational world, as well. Our mission is to use this virtual reality equipment to bring mathematics to life in a way that any curious mind can appreciate, regardless of their experience level. Over the course of the semester, we developed a roller coaster on the Unity Game Engine, where users embark on a tour of 6 different topological surfaces to better understand the idea of orientability in a fun, interactive way. Orientability can be defined as the ability to make a consistent choice of an outward vector normal to the surface. When thinking in terms of an ant travelling along the surface, a non-orientable surface is one in which the ant can traverse every part of the surface simply by walking forward. A classic example of a non-orientable surface is the Mobius band. In our game, you are the ant. The addition of a flip command allows one to distinguish between orientability and non-orientability. Just like the ant, if you explore every part of the surface without pressing flip, you are on a non-orientable surface. This game is compatible with the Oculus Rift and Mac computers, and is free to download under the ‘Visualization’ tab, so we encourage you to try it out!

In the 1950s Nash and Kuiper proved the existence of an isometric embedding of a flat torus in 3D Euclidean space; however, they did not provide a visualization of such embedding. In the 70s and 80s, Gromov developed the convex integration technique, providing the tool for such construction. From 2006 to 2012, three French mathematics institutions collaborated in the Hevea Project to produce a 3D model of such embedding. Our initial attempt to replicate the Hevea Project solution was inspired mainly by the convex integration technique: wrapping a high-frequency but small-amplitude sine wave around a unit circle. In order to achieve the convergence to the unit circle and the desired arc length, the amplitude was decreased as the frequency increased accordingly. Unfortunately, the first derivative did not converge as the frequency approached infinity. During the semester, a new construction, inspired by the self-similarity and fractal structure of the Hevea Project solution, was created to correct the initial shortcomings. In this new technique, which we call the sinusoidal fractal, increasingly higher frequency sine waves were wrinkled normal to previous iterations, instead of corrugating along a single direction. We proved that this construction satisfies all three conditions for an isometric embedding from 1D to 2D. Utilizing sinusoidal fractal curves, we constructed a model of the isometric embedding of a flat torus in 3D and produced a physical visualization using a 3D printer.
Download the Flat Torus STL here: Flat Torus STL file

Between August 4 and November 19 MEGL Outreach ran 7 mathematical enrichment activities at 6 locations from Virginia to Illinois, reaching over 130 students and guests. The participants ranged from kindergartners to high school students with a broad range of mathematical ability. Together we we danced through the complex numbers, used balloons to break the rules of Euclidean geometry, and crocheted our way into negatively curved spaces.
Also during this time Director Sean Lawton and Outreach Coordinator Jack Love developed a new activity to be launched in Spring 2016, called Really BIG Numbers, where elementary school students gain a first-hand intuition for just how big numbers can get. Spoiler alert: thousands of ping pong balls are involved.
