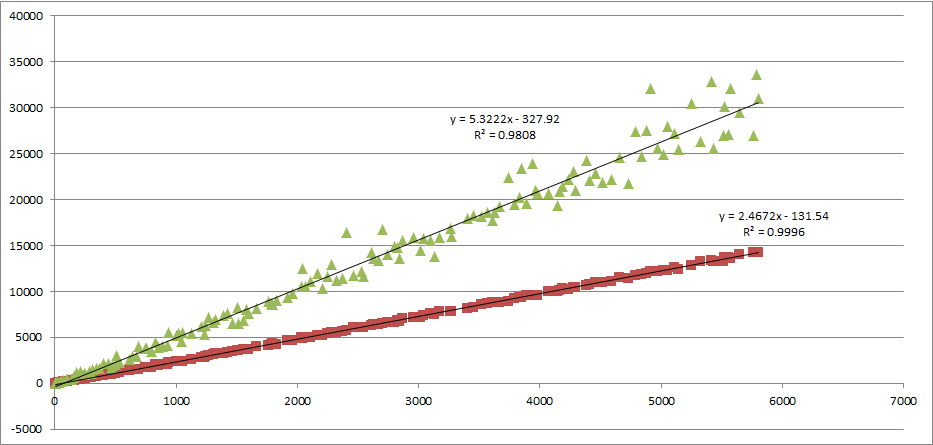
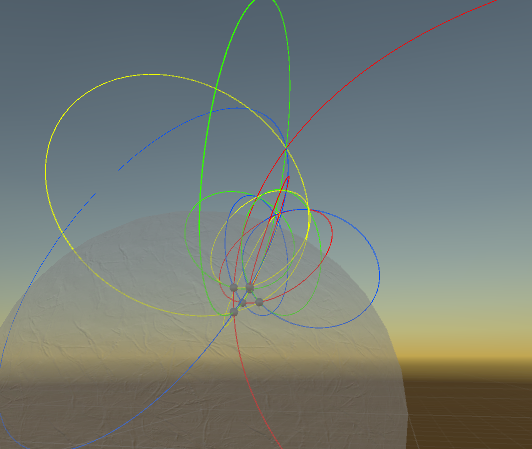
During Summer 2017 MEGL ran a small program with 7 participants. There was one research group (Orbits), one visualization group (Hyperbolic Virtual Reality), and one public outreach group (Outreach). The research and visualization groups engaged in experimental exploration involving faculty and undergraduates. Teams met weekly to conduct experiments generating data, to make conjectures from data, and to work on theory resulting from conjectures. The outreach group involved faculty, and a graduate student to develop and implement activities for elementary middle and high school students. We concluded with final reports from all teams at the Geometry Labs United Conference at the University of Washington.
The automorphism group of the polynomial $k(x,y,z)= x^2 + y^2 + z^2 – xyz – 2$ over a finite field $\mathbb{F}_{q}$ has a subgroup $\Gamma$, consisting of polynomial automorphisms, whose orbit lengths are of particular fascination. The group $\Gamma$ is generated by the automorphisms $\iota$, $\tau$, $\eta$ and acts on the variety $\mathbb{V}(k – \lambda)$, for $\lambda$ in $\mathbb{F}_q$. We are interested in the length of the longest orbit, denoted $\mathcal{L}_{\langle w \rangle} (q, \lambda)$, for a fixed $\lambda$ and prime power $q$, where $\langle w \rangle$ is the cyclic subgroup generated by $w$ in $\Gamma$. The evaluation of our $\mathcal{L}$ function is complete for $\iota$, $\tau$, $\iota \tau$, and $\eta \iota$. [[f<image graph.png size=”small”]] A motivating conjecture is that these automorphisms will act transitively (in a certain measure sense) on the variety as $q$ tends toward infinity. We hope to gain insight into how the group action is approaching transitivity by studying automorphisms of exceptionally large order. The automorphism $\eta \tau$ is of interest due to its orbits rate of growth as $q$ increases. It appears to tend toward $q \log{q}$. This is significantly larger than the linear growth rate of $\eta$, or the constant orders of $\iota$, $\tau$, $\iota \tau$, and $\eta \iota$.
During the summer, the VR team worked on setting up a robust system of hyperbolic isometries (the group of isometries is $ \mathrm{PSL}(2,\mathbb{C})$, the group of Möbius transformations), in the Unity game engine. In order to do this, we created classes that encoded the algebra of complex numbers and matrices. Using that, we programmed Möbius transformations (defined on the 3 dimensional subspace ${ z+jt | z\in \mathbb{C}, t \in \mathbb{R} }$ of the algebra of quaternions) and sphere inversions. Lastly, we set up a way to render polyhedra and apply isometries to them. Using these constructions, an application that lets the user apply isometries to a tetrahedron was made. Some progress was made on building a lattice of hyperbolic polyhedra.
Download our Oculus Rift App.
This year was MEGL Outreach’s biggest Summer so far. We held 5 events at 4 locations and reached over 250 students. We ran Really BIG Numbers for elementary school students at the Fairfax County Association for the Gifted; we ran Your Teachers Are Lying to You for 4 classes of students at Robinson Secondary School; and we ran Snowflake Symmetry for 35 elementary school students at the San Francisco Math Circle Math Camp in California, and 90 elementary and middle school girls at FOCUS Camp (Females Of Color Underrepresented in STEM) at GMU. We also continued to expand our network of local schools and libraries and are looking forward to a busy Fall calendar.